Soaring – Chess in the Air

At my club, the Soaring Society of Boulder, we are trying to help freshly minted glider pilots who are eager to develop their skills but are unsure how to go about it.  Stats show that a large percentage of recently-trained pilots exit our sport long before they have experienced what’s possible.  However, those who reach for the challenge, often find a passion that lasts a lifetime.

I believe that one key tool that can help a new pilot’s development is a set of standardized soaring tasks.  In the case of Boulder, we carefully designed them for our demanding mountain soaring environment. It’s paramount that pilots stay safe as they progress. This article introduces these tasks – from Beginner to Diamond.

You can find much more detailed information about these tasks here.

From Beginner to Silver

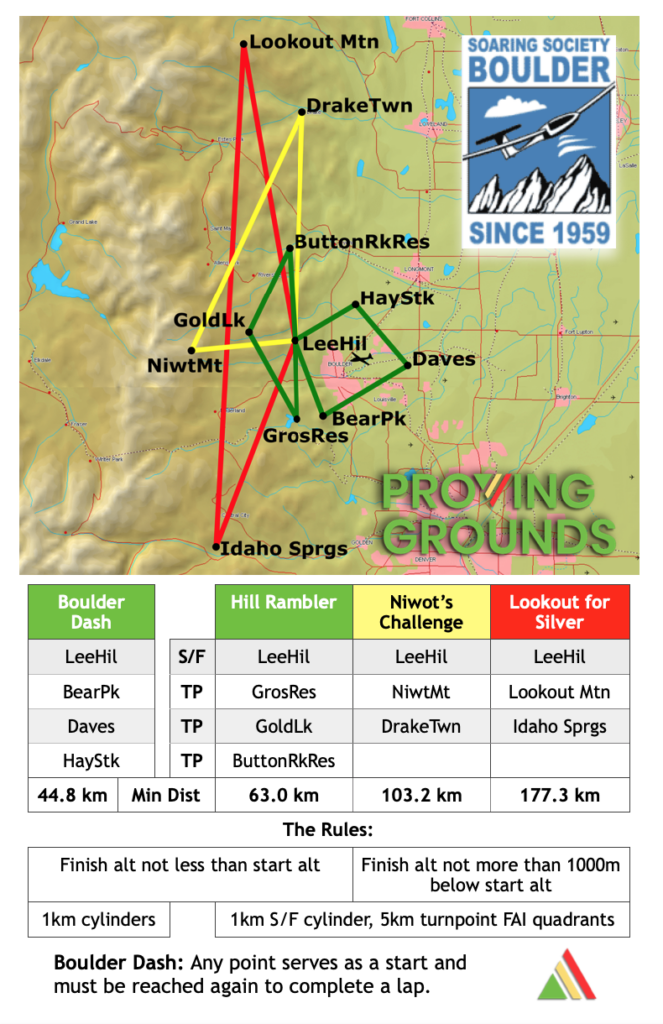
Our first task is called “Boulder Dash.”  It is a ~45 km flight around the city of Boulder and takes the pilot never further than 12km (7.5 miles) away from the airport.  It is suitable for any licensed pilot who is able to stay airborne on a good soaring day.  In addition,  the pilot must have the mental bandwidth to maintain situational awareness.  E.g., they must pay close attention at all times to other traffic and airspace constraints.

The tasks build on one another and are getting progressively harder.  “Hill Rambler” introduces pilots to mountain flying over the foothills of the Rocky Mountains.  It also doubles the distance away from the airfield.  However, pilots can easily keep the takeoff airport within safe glide at all times.

“Niwot’s Challenge” takes pilots close to the Continental Divide, the spine of the Rocky Mountains.  Pilots learn to carefully manage their altitude to ensure the safety of the flight at all times. The second turn point doubles again the distance away from Boulder. Pilots must consider other landing options should it become necessary.

“Lookout for Silver” builds on everything pilots have learned in the prior three tasks.  Pilots can earn Silver Distance and Silver Altitude – two of the three components of the Silver Badge.  Total task distance is 170 km – a great preparation for earning their other badges.

Proving Grounds Support

These first four tasks will be supported by Proving Grounds.  Proving Grounds is a platform developed by a group of Canadian soaring pilots.  It is super easy to use and provides a low maintenance approach to member development. The Soaring Society of America supports its adoption in the US.  This may be a great opportunity for your club!

Pilots who complete any one of these four tasks can simply email the .igc trace to a “bot” which automatically scores their flight.  Pilots can then post their achievements on a stainless steel task board.  The board will be mounted at the airfield and lists the flights ranked by average speed achieved (adjusted for glider handicap).  The bot provides all the relevant information.

In addition to support by Proving Grounds, our club will provide individual task sheets.  These contain task-specific safety tips (e.g. suggested minimum altitudes, air traffic pointers, potential terrain traps) as well as tactical advice regarding weather, soaring conditions, and how to fly each task.  Pilots are also encouraged to become proficient in the use of a flight recorder – a key requirement for earning their badges.

Our support program does not end there.  The next step is for pilots to work on their Gold and Diamond flights.

Gold and Diamond

“Gold in Glide” is aptly named because this task allows pilots to earn their Gold Distance requirement while staying in glide range of the home airport the entire time.  This is possible thanks to our topography, outstanding soaring conditions, and our club gliders.  During the summer, we can routinely soar to just below Class A airspace (which starts at 18,000 feet).  Our club’s two Discus CS gliders are ideally suited for accomplishing all badge tasks.

“Front Range Diamond Goal” and “Front Range Diamond Distance” are task recommendations for pilots who have completed their Gold Badge and are ready to leave glide range for the first time.  However, other airports near the proposed routes help pilots stay safe.  These tasks are mere suggestions: pilots are encouraged to adjust their tasks based on the day’s specific weather conditions, e.g. taking advantage of particular energy lines (such as the typical Front Range Convergence).

Our club encourages flight instructors and experienced cross country pilots to support aspiring pilots with ground-based coaching.  Some may even fly some of the tasks with them in our club’s DG 505 or via lead-and-follow mentoring.

The goal is to give pilots a framework and support to embrace the challenge of developing from glider pilots to XC mountain soaring pilots without putting themselves in danger.  It may lead to more pilot engagement and long-term retention of valuable club members.

Here’s a link to download a presentation with detailed descriptions of all tasks.

If your club has also taken steps (similar or different) to help pilots cross the gap from freshly certificated glider pilot to safe cross-country pilot, I’d love to hear from you in the comments or via email at chessintheair@gmail.com.

(Editorial Note: since initial publication, I have added a few thoughts suggested by readers.  Andy Blackburn’s input has been particularly valuable.  I also added a post scriptum at the end with additional tips.  Thank you to all who commented.)

Who has not heard of the MacCready Speed-To-Fly Theory?  It is the brilliant discovery of a brilliant man who was not only the first American to become a world soaring champion but who came up with a scientific way to demonstrate how fast we should be flying in-between thermals in order to maximize our cross-country speed.

Not long after MacCready published his theory, other pilots followed his example and began equipping their gliders with “MacCready Rings”.  These are simple devices mounted around a glider’s variometer telling  the pilot how fast they should be flying depending on the expected strength of the next lift.

With the onset of flight computers, MacCready’s Speed-To-Fly Theory (or STF for short) went digital.  Today, every flight computer requires the pilot to input their “MC value”,  and every STF vario will produce audio and visual signals. These tell the pilot whether to speed up, slow down, or maintain the current speed – based on the MC value they selected.

Over time the application of STF theory has evolved a bit.  E.g., pilots have learned that it is useful to slow down as they get closer to the ground to minimize the risk of a landout.  Others correctly pointed out that “chasing the needle” is not only distracting but that constant control inputs make it inefficient as well. Instead, most would recommend flying at “block speeds” that approximately correspond to the correct MC setting.  After all, flying a bit too slow or a bit too fast makes little difference in terms of the average speed achieved. Some have even come up with scientific ways to show when, how, and how much to deviate from MacCready’s theory. (E.g., see Daniel Sazhin’s and John Bird’s work about “Bounded Rationality and Risk Strategy in Thermal Soaring” or John Cochrane’s article, “MacCready Theory with Uncertain Lift and Limited Altitude“).  Instead of getting into more details here, I recommend that interested readers take a look at the article “Just a Little Faster, Please“, also by John Cochrane.

However, no-one doubts that MacCready theory at its core is mathematically correct and scientifically sound.  It remains the undisputed foundation of any theory about how fast we should fly in cruise.  Most importantly: every flight computer and every vario asks you to input an MC value.  So you better know what these devices are doing with the information you enter.

MacCready Theory in a Nutshell

Every soaring textbook has an explanation for how and why the theory works. In essence, it is quite simple: when the lift ahead promises to be strong you should fly faster.  When the lift ahead looks to be weaker, you should fly closer to your glider’s best L/D speed, i.e. the speed where it has its best glide ratio.  MC theory tells you exactly how fast you should fly based on the strength of lift you expect ahead.

The series of charts below illustrate a simple example.  They are based on the speed polar of a Discus CS (one of the most popular standard class gliders) without water ballast.  (The principles explained are the same for whatever glider you fly but the values will obviously differ. If you fly a similar glider, such as an LS4, a DG 300, or an ASW 24 they will be close. A DG 505’s polar is also similar.) The speed polar is the curved line in blue.  It illustrates the rate of sink at various speeds.  The speeds are on the horizontal axis (in kts), and the glider’s rate of sink at these speeds is shown on the vertical axis (also in kts).  Using the same units on both axes (in this case kts) is very helpful because you can calculate the glide ratio at any point along the curve simply by contrasting the speed to the sink rate.

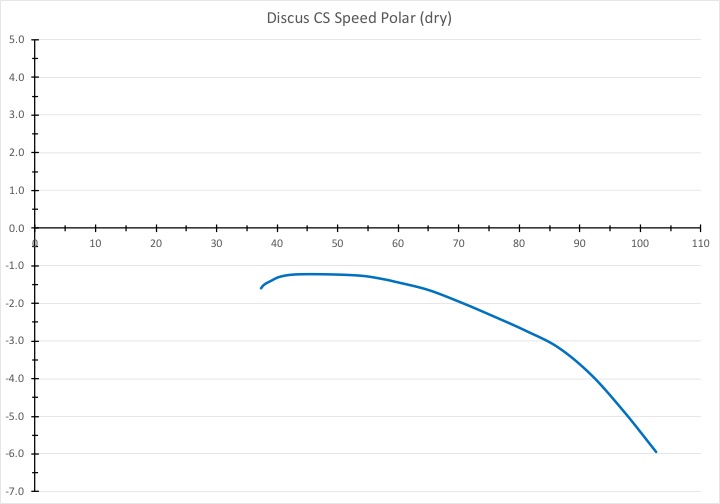
The next graph below shows that the best glide performance of the Discus CS is at about 55 kts. You can find this best glide speed by placing a tangent (the red line) against the speed polar starting at the chart’s origin (the point 0,0).

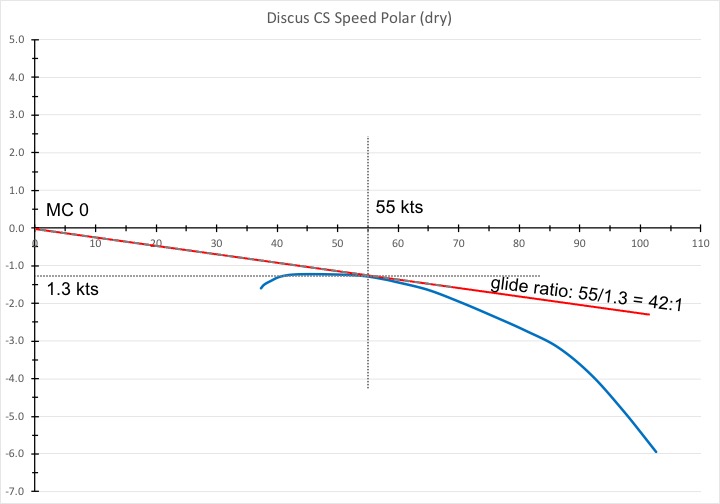
At 55 kts the Discus will sink at a rate of 1.3 kts.  55 divided by 1.3 equals 42.  55 kts is the best L/D speed for a Discus and its best glide ratio is 42:1.

The only time you would ever fly at the best glide speed is when you are desperate.  Let’s say the lift has died for the day, the air is completely still, and you are just high enough to safely make it to an airport.  That’s when you would fly at best L/D.  This speed is also called MC 0 speed:  the expected strength of the next lift is zero (because you know there is no more lift to be had) and all you are trying to do is to stretch your glide as far as possible.

Let’s look at a more frequent example.  It’s a pretty strong day.  You are high and there are several good-looking cumulus clouds ahead. During the last few climbs you achieved 4-5 knots on average from the bottom to the top of each thermal (including any centering delays, re-centering efforts, etc) and you expect the next lift will be just as strong.  In this case it makes sense to set your MC to 4.  You expect the next lift to be just as strong and you are not willing to stop for anything less than that – at least for now.  In this case you should fly at MC 4.  (MC 3 or MC4 are perhaps the most common MC settings that pilots use for Speed-to-Fly calculations.  Higher settings only make sense in exceptionally strong conditions. How often would you not take a climb that averages 4+ knots from bottom to top?)

You simply feed MC 4 into your vario and it will tell you to fly at MC 4 speed.  The chart below shows you how your vario calculates this speed:  it places a tangent (once again the red line) along the speed polar curve but this time it starts at a point 4 knots above the origin.  The tangent touches the speed polar at 83 kts and you can see that at this speed the glider will sink 2.9 kts per hour.  The glide ratio at this speed is 83/2.9 = 29.  I.e. you will glide 29 ft forward for every 1 ft of altitude you lose.  29:1.

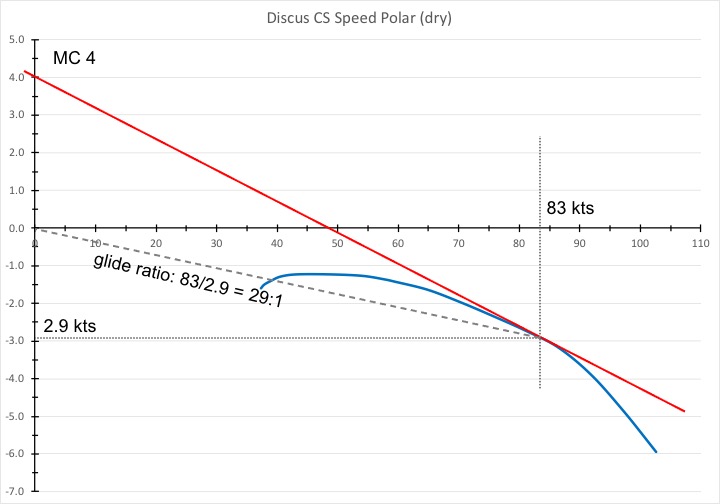
OK, so far, so good.  You already knew this anyway.  But what does this have to do with the headline?  Where’s the peril?  That’s what we’re getting to now.

The Other Use of the MacCready Value

The MC value that you enter is not only used by your vario to calculate your best Speed To Fly but it is also used by your flight computer to calculate whether you can safely reach a place to land.

I very much doubt that this was Paul MacCready’s idea.  But that’s how your flight computer works. And if you don’t know it, it can be a big problem!

In the example we just discussed above it is hard to see.  When you’re flying high and happy and are confident that the next thermal will deliver a 4 kt average climb you are probably not too concerned about reaching a safe place to land.  And if you glance at your flight computer it will use your MC 4 setting to calculate which airports (or landout fields) are in safe glide at MC 4.  I.e., it will do so based on a glide ratio of 29:1.

But let’s say the expected 4 kts of lift did not materialize.  In fact, the clouds that looked so good before are now dissolving and you’re getting lower and lower.  Far from being confident that the next lift will deliver 4 kts, you are gradually getting concerned.  And, as you should, you dial back your MC settings.  First to MC 3, then to MC 2, and, as you get lower and lower, you move it back to MC 1. Eventually you are getting desperate and dial it all the way back to MC 0.

This makes sense because you want your STF vario to tell you to fly more slowly so you better conserve altitude and have more options to find lift ahead, rather than driving hard down to the ground.

But what does your flight computer do with the same information?  As you reduce your MC settings to 3, 2, 1 and then to 0, your glide computer thinks you can glide farther and farther.  It basically removes your safety margin.  Remember: at MC 0 your flight computer believes you are able to consistently  fly at the very optimal glide speed – 55 kts in still air – and achieve a glide ratio of 42:1. Is this realistic? Probably not.

By reducing the MC value to 0 you just told the glide computer to lie to you.  It is now showing airports (or fields) in glide range that really aren’t.

But things are probably even worse.  Quite possibly much worse!

Unless the day has truly died and the air become completely still, chances are that the airmass you are flying through is actually going down.  Why?  Because as long as there are thermals and the air is going up somewhere, it must be going down elsewhere.  Completely still air hardly ever exists and it most definitely does not exist on a day when we expect to find enough lift to fly cross-country.

So let’s say the air you’re flying through is actually going down by 1 kt.  One knot is not much and definitely not unusual. What are the implications?

Well, first of all you should be flying a bit faster.  When the air is sinking at 1 kt, your STF vario will tell you to speed up even if you leave your MC setting at 0.  How does it do this?  Easy: 1 kt sink will simply shift the glide polar down by 1 kt because you have to add the sink rate of the airmass to the sink rate of the glider.  (The vario obviously knows you are in sink and it does this automatically. ) You can see the new polar on the chart below (in orange).  You can also see where the tangent touches the new polar curve.  This point is at 59 kts and your sink rate will now be 2.4 kts.  (In still air it would be 1.4 kts but since you’re in 1 kt sink, so you’re actually coming down at 2.4 kts.)

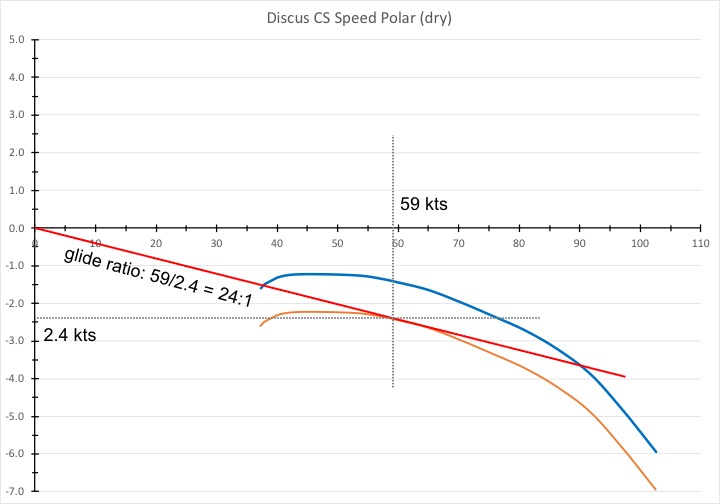
Now, look at what happened to the glide ratio!  At 59 kts and 2.4 kts sink, your glide ratio is now 59/2.4 = 24:1.   You’re still flying a high performance glider but just 1 kt of sink is enough to basically turn it into a Schweitzer 1-26!

What about the safety glide calculation?  Your glide computer does not know how long the sink will last so it does not take it into account at all!  (This makes sense because otherwise the safety glide calculation would jump around wildly each time you fly through a bit of lift or sink.) Remember this! The flight computer will account for wind (because wind doesn’t change from second to second) but it does not account for lift or sink when it calculates which airports (or fields) are in glide.

So what does it tell you?  Since you turned down the MC value to 0, it will calculate your safety glide with a 42:1 glide ratio even though you are only achieving 24:1!

It is easy to see why this is at best misleading, and at worst a major safety hazard.  A lot of beginning XC pilots tend to use what they think of as a “conservative”, i.e. low, MC setting.  As long as this is only applied to Speed-to-Fly calculations it makes sense because it helps them stay high (while obviously slowing them down).  But when applied to safety calculations a “low” MC setting is just the very opposite of conservative!

What Should You Do?

Now that you understand that your MC settings are used for two completely different purposes – calculating your speed to fly, and calculating your safety glides – what can you do about it?

The answer is simple: use two different MC settings, each appropriate for its purpose!

If your glider has an electronic Speed-to-Fly vario and you are also using a completely separate flight computer with a moving map, things are straightforward. For the vario use an MC setting that’s based on the minimum strength of the lift you are willing to accept.  For the flight computer use an MC setting that’s appropriate for safety glide calculations.

This describes the setup that I was flying with last year.  I had an STF vario in the panel and a stand-alone Oudie IGC flight computer with a moving map display.  I entered my STF MC setting into the vario, and kept a different (usually higher) MC setting on the Oudie.  This way the Oudie would only show me airports and fields that really were in safe glide range.

Things get problematic when your STF vario and your flight computer are connected with one another. Changes that you make to your MC settings on one device are probably automatically sent to the other device. The two devices are kept in synch.  This seems like a great convenience but in reality it is anything but!  In real life it is quite rare that you want to use the same MC value for your STF calculations and for your safety glide calculations. And whenever it is appropriate to use two different values than either of these two calculations will simply be wrong!

If you use a setup where your SFT vario and your flight computer are connected with one another (e.g. via cable or bluetooth), see if there is a setting that prevents the two devices from synchronizing MC values.  You want each of these devices to correctly calculate the thing it is supposed to calculate!

If you only use only one single device for both STF and safety glide calculations (or if you cannot prevent your STF vario and your flight computer from synchronizing MC values) you must remember to edit your MC setting based on what you want to focus on. If you are relatively new to cross country soaring I suggest that you set the MC value appropriately for safety calculations and simply ignore your vario’s speed-to-fly suggestions.  You’re probably not going to fly as fast anyway as the vario suggests you should.

And there’s one additional thing you should do:  make sure that you complement a safe glide calculation by also setting a safe arrival altitude.  After all, you don’t want to arrive at the airport (or field) at grass root level. You want to have enough time to do a proper landing check and fly a safe landing pattern.  What’s a safe arrival altitude?  That is a different question for another time.  In Boulder, I always plan to arrive no lower than 1500 AGL because we have a very busy airport, and I may be in line behind other gliders or even a bunch of skydivers that are floating above the field just when I get there. Extreme weather can create problems, too.  Here’s a scary experience from a few years ago.

What MC Value is Appropriate for Safety Glide Calculations?

We know from the MacCready theory how to set MC for Speed-to-Fly calculations:  enter the expected lift of the next thermal.  Better still (since you don’t really know how strong the lift ahead will be): enter the minimum strength of lift that you are willing to take right now.

But how to set MC for calculating safety glides?  Well, as always, it depends. Since this calculation is about safety, and only about safety, the key question you should ask:  given the looks of the conditions ahead, what is the “worst-case glide slope” with your glider in the direction you’re heading – at least until the next landable field or airport?  Whatever your estimate is, you can then enter an MC value that corresponds to that glide slope.

OK, so how do you estimate your worst-case glide slope?

We have seen above that sink has a very negative impact on the attainable glide slope.  Just 1 knot of sink will turn a 1:42 glider into a 1:24 glider.  What about 2 knots of sink?   Let’s take another look at the speed polar.

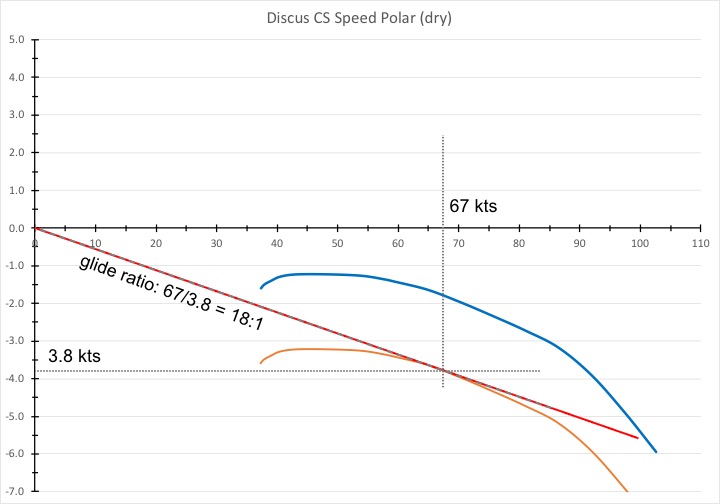
Two knots of sink will shift the speed polar down by – you guessed it – 2 knots.  You’re in sink, so you must fly faster.  How fast? Place a tangent from the origin against the new (orange) speed polar.  67 knots is the speed to fly and your rate of sink will be 3.8 kts.  In the best case, this equates to a glide ratio of 18:1.  (I say best case because it is pretty difficult to fly exactly at the right speed to fly and if you fly a little faster or slower, your glide ratio will actually be worse than 18:1.)

Depending on where you fly, two knots of sink still isn’t all that bad.  Here in Colorado it is not uncommon to hit pockets of sink where the air goes down by 5 kts or even 10 kts.  In wave conditions it could be as much as 20 kts!  How would that affect your glide slope?

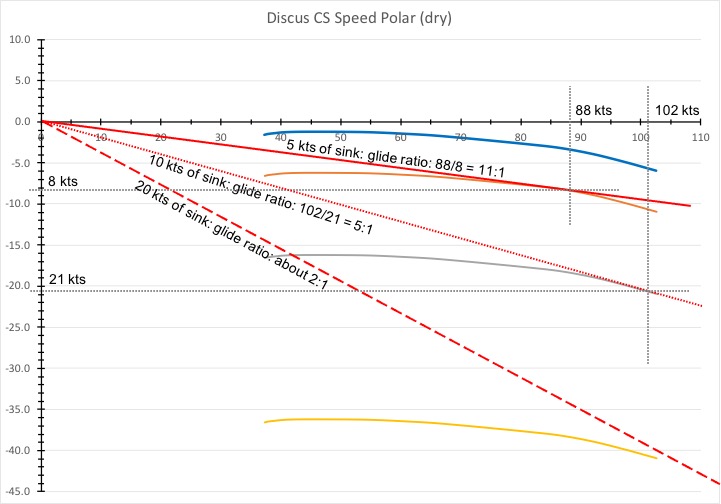
The chart above shows that the impact of strong sink is downright frightening.  If you fly through 5 kts of sink your best glide ratio is 11:1 at a speed of 88 kts.  If you cross 10 kts of sink, your best glide ratio becomes 5:1 at a speed of 102 kts.  And at 20 kts of sink, the answer is literally off the chart. You’d fly somewhere between rough air speed and Vne and you’d be lucky to achieve much better than 2:1.

Scared? Well, you should be.  Big sink is scary.  If feels like you’re coming down like a brick.  Because you are. Well, almost.  Fortunately, strong sink tends to be short-lived.  And since it’s true that what goes up must come down, it’s also true that what comes down must go up.  Strong sink and strong lift tend to exist in close proximity to one another.  Wave flying is an extreme example where 10-20 kt lift and 10-20 kt sink can be within 1 or 2 miles from one another.  Try to get out of sink and back into lift as soon as possible! Hopefully you know what you’re doing!  Or, perhaps even better: think twice before you decide to fly in such extreme conditions to begin with.  The point is that such extreme scenarios are not really all that helpful when you decide how to program your flight computer.

In regular summer soaring conditions the more typical cases are that you’re getting low because the lift is weakening, that you fell out of the lift band, or that you crossed into a slowly descending airmass.  In Boulder, Colorado, a classic example for the latter is that you fell out of the convergence, can’t get back, and are struggling to find good lift in the eastern airmass. A divergence zone running parallel to the convergence may put you in sink.  In these cases you are unlikely to be confronted with sustained strong sink.  But even in relatively benign conditions, it is still quite possible that you experience an average of 1 kt of sink on your final glide home.

Lets revisit the chart for 1 knot sink.

As we saw before, at 1 kt sink we should fly 59 kts and our glider will sink at a rate of 2.4 kts.  Our glide ratio will be 24:1.

If this is the “worst-case glide-slope” that we are expecting, how can we instruct our flight computer to make the appropriate safety calculation?  The answer is: we have to find the MC setting that corresponds to a 24:1 glide slope in the absence of lift or sink.

The following chart shows how we can do this easily.

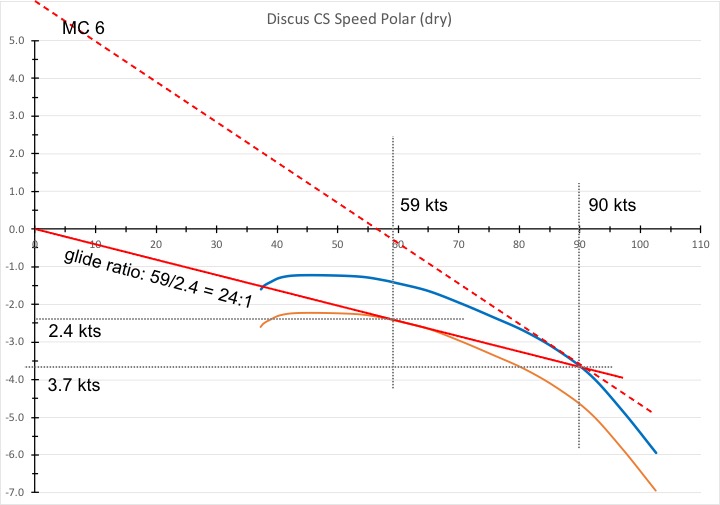
We simply look for the point where the 24:1 glide slope line (i.e. the red tangent to the orange speed polar) intersects the original (blue) still-air speed polar.  We find that this point is at a speed of 90 kts and a sink rate of 3.7 kts.  Now we draw a new tangent (the dotted red line) that touches the blue polar at exactly this spot. Then we check where this new tangent intersects the vertical axis. You can see that for the Discus this point is at 6 kts.  In other words: if we expect a worst case glide slope of 24:1 all the way to the airport (i.e., conditions that reflect 1 kt of sink), we should set MC to 6.

You might be interested what MC setting I use.  Once again, it depends!  If there is a well-marked energy line ahead that I can follow, e.g. a cloud street or the typical Rocky Mountains convergence line, I am comfortable to base my safety glide ratio on an MC value as low as 3.  If the sky is blue and I don’t really know what to expect I tend to use MC 4 or 5.  And if the terrain is particularly hostile I bump it up to 6 or 7. Ultimately, it comes down to a judgement call.  The more doubt I have about the conditions ahead and the greater the probability of sink, especially prolonged sink, the higher I set my MC value.

If you’re flying in particularly challenging terrain or if you’re not yet experienced in avoiding areas of persistent sink, you may want to follow the advice of the French mountain soaring team and use a “worst-case glide ratio” that is 1/2 of your gliders best glide performance. For the Discus CS this glide ratio is 21:1.  The chart below shows that a Discus (without water ballast) will achieve 21:1 at a speed of 95 kts when the corresponding sink rate is 4.5 kts.  And the corresponding MC value is about 10.

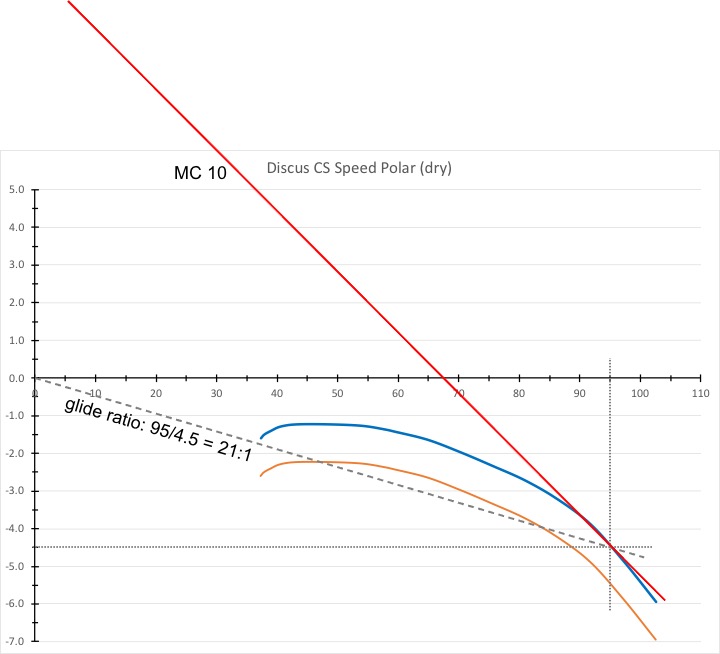
Remember that estimating a “worst-case glide ratio” is by no means a guarantee that reality may not be harsher yet.  Perhaps even much harsher.  I have shown above how bad a glide ratio gets if you hit 5, 10, or even 20 knots of sink!

Conclusion

The purpose of this article was to make clear that your glider avionics use MC for two completely different purposes and that applying inappropriate values can have dangerous unintended consequences.

Your STF vario uses MC to calculate the best speed-to-fly based on your assessment of the strength of lift ahead.  If you’re conservative, you want this value to be lower, not higher.  This will make you stay relatively high albeit at the expense of a somewhat lower cross-country speed. Irrespective of your level of experience, the most appropriate MC value is, “what is the weakest lift that I would be willing to accept right now.” MC 2, 3 or 4 are fairly typical.  Only in exceptionally strong conditions will it be 5 or higher.

Your moving map flight computer uses MC to calculate which airports or fields are within safe gliding distance.  If you’re conservative, you want this value to be higher, not lower.  This will force you to stay high enough that you can safely reach your destination even if you should face less than favorable conditions ahead. Your skills, experience, the terrain, and the conditions of the day are all important factors to consider when you set this value.  On benign summer days a value of MC 5 or 6 may be appropriate.  If you’re inexperienced, flying over hostile terrain, or if you are unfamiliar with a particular soaring area, MC 10 will give you an extra safety margin. And always complement your glide slope calculation with a safe arrival altitude so you have the altitude you need for a safe landing pattern.

Importantly, set your MC values separately for  your STF vario and your flight computer.  Prevent these devices from synching their respective MC values if at all possible.  Be very careful if you only use one device (or one synchronized input) for both calculations.  The biggest trap exists when you dial back your MC setting for SFT purposes and your flight computer stretches your attainable glide unrealistically farther and farther.

Even the highest possible MC setting will not be appropriate to calculate safety glides when extreme sink, or strong sustained sink, is possible. When conditions are extreme, the best advice is to stay really high at all times.  And if that’s not possible, or if you’re not sure you can deal with the conditions at the time, you can always decide to fly on a different day instead.

Have fun and fly safe!

Post Scriptum

There has been a lot of interest in this article.  Within 48 hours of publication it has been read about 2,500 times and a lot of readers made excellent comments, either below or on social media.

First of all they confirm that the trap is real: entering a low MC value into your flight computer will result in wildly over-optimistic glide slope calculations and show fields or airports within glide range that really are not. However, there are multiple ways to avoid the trap and my suggestion in the article of using a different (and higher) MC value for safety glide slope calculations is only one of them.

Below I want to summarize a few comments that I found particularly helpful:

• If the terrain in your soaring area is generally landable there is not all that much to be concerned about.  E.g., one pilot from the Netherlands commented that where he flies there are always several landable fields in glide even from as low as 1000 AGL.  If that describes your soaring terrain then this topic doesn’t really apply to you.  Your main challenge may be to resist the temptation to keep trying to find lift until you’re very close to the ground.  Delaying the decision to land until it is too late for a safe landing is the #1 reason why glider pilots get killed. This is a different topic. You can read more about it here.
• As an alternative to using MC inputs for your final glide calculation you may be able to use “Required L/D”.  E.g., I have my Oudie set up to display two Nav boxes at the top of the screen: “Required L/D” and “Current L/D”.  As long as my “Current L/D” exceeds the “Required L/D” I am gaining relative to my required glide slope and my odds of making it to the target improve.  Conversely, if the “Current L/D” drops below the “Required L/D” I am losing against my required glide slope and may be in trouble.  This is a very useful method.  If you use it, it is critical that you also complement it with a safe arrival altitude. In this video, I show an example of a final glide back to Nephi, Utah where I needed a glide ratio of 25:1 to get back to Nephi but then my “Current L/D” temporarily dropped to 18:1.  (I was flying my 48:1 Ventus 2.)
• A lot of excellent pilots don’t use a “Speed-to-Fly” vario to tell them how fast to go.  Instead they primarily rely on “block speeds.”  E.g., if they are high and feel “confident” of finding good lift they will fly at a speed that roughly corresponds to their gliders STF at an MC setting of 4 in still air.  If they are getting towards the bottom of the best lift band they become “conservative” and fly at a speed that corresponds to MC 2.  And when they get “desperate” and are really looking for lift, they slow down to a speed corresponding to MC 1. And if they are “feeling lucky” high under a strong cloud street they fly extra fast.  One of the commenters calls it “warp” speed.  For a dry Discus CS these speeds might be: desperate: 60 kts; conservative: 65 kts; confident: 75kts; warp: ~85-90 kts.  Add about 10 kts to each speed when flying with water ballast.  If you like this method there is no need to mess with your MC value at all.  Simply set an MC value on your flight computer that’s appropriate for your safety glides (combined with a safe arrival altitude) and leave it at that.
• Similarly, if you like your STF vario set to “netto” instead of “Speed-to-Fly” you also don’t need to bother meddling with MC values during the flight, and can just use an appropriate MC setting for safety glides on the flight computer.
• What MC value is appropriate for safety glides varies with the soaring terrain.  My article was written from a mountain flying perspective.  Where I fly in Colorado it is common that the next landable airport or field is 20, 30, 40, or even 50 miles away and soaring conditions tend to include strong lift as well as strong sink.  Talk to experienced pilots in your area to understand what safety glide ratio (and hence what MC value) may be appropriate for where you fly.

Keep the comments and insights coming.  Soaring is an unforgiving sport and our safety largely depends on our ability to learn from the mistakes others have made before us.  (Or on sheer luck – but only for as long as it lasts.)  By learning together we’ll become better and safer pilots.

Having reviewed my progress against the Soaring Goals that I had set for 2020, the last day of the year feels like a good time to publish new goals for 2021.

So here’s what I’m aiming for:

1. Stay Safe by always heeding my own advice.

2. Improve Specific Flying Skills, based on this analysis of a race day in Nephi, this analysis of the Speed League Season, and the advice from soaring GOAT Sebastian Kawa, who emphasized that we must learn to fly very precisely if we want to be fast.

• • • Netto in cruise.  Sharpen focus on following energy lines, measured by consistently achieving above-average netto values in cruise flight, a much better metric than circling percentage and effective glide ratio.
    • Altitude band.  Use more of the available altitude band to become more selective in thermal acceptance.  This will require an adjustment of my flying style.
    • Precision thermalling. Focus on quick centering, maintaining optimal coordination, circling speed, and 45 degree bank angles.  As a result, achieve above average climb rates when compared to other pilots flying in the same area on the same day.

3. Speed Goals. Apply these skills to achieve the following:

• • • When flying on Speed League Weekends aim to score among the top 3 Boulder pilots 66% of the time (up from 50% in 2020).
    • Try to break one of the Open Class Colorado Speed Records (stretch goal).

4. Distance Goals.  Weather permitting, I would like to achieve two of the following in 2021:

• • • Reach one additional U.S. State flying from Boulder: New Mexico, Utah, or Nebraska.  An aspirational stretch goal is a “border to border” flight from Boulder to New Mexico, then to Wyoming, and back to Boulder.
    • Complete a 1000 km flight per OLC plus rules.
    • Complete a 750 km FAI triangle or a 1000 km Diplome.
    • Add to my 14er bag with a flight to the southern-most peaks of the Sangre de Cristo Range or a flight into the San Juan Mountains.

5. Contest Goals.  I plan to fly at least three or the following four contests:

• • • Region 7 in Albert Lea, MN (May 17-22)
    • 20m 2-seater Nationals in Montague , CA (Jun 14-22)
    • Region 9 or 18m Nationals in Nephi, UT (Jun 29 – Jul 8)
    • Region 10 in Uvalde, TX (Aug 15-21)

Since these are my first contests, I want to focus mainly on skill development, flying consistently, and completing as many tasks as safely possible.  Stretch Goal: place in the top 33% at one of the Regional Contests or in the top 50% at a Nationals Contest.

6. Giving Back.  I will continue to put energy towards inspiring others worldwide to join our sport, to develop, excel, and stay safe.  I will do this through:

• • • Writing – follow me on ChessInTheAir.com and on Facebook
    • Presentations and Podcast Contributions – to local, national, and international audiences
    • Videos – subscribe to my ChessInTheAir YouTubeChannel, and
    • Serving for soaring organizations such as the Soaring Society of Boulder

I wish everyone a Very Happy New Year!

Stay safe, and may your soaring goals come to fruition.

This time last year I was in the midst of negotiating the purchase of my first glider: a beautiful Ventus 2cxT.  It was “almost like new” with only 500 hours.  Early in January I closed the deal and drove to Dallas, Texas for a final inspection. Having found that everything was indeed tiptop, I was excited to tow it home to Colorado.

In February I travelled to the SSA convention in Little Rock, Arkansas.  Attending seminars and seeing all the shiny new objects on the convention floor I was excited for the soaring year ahead.  I also met with Daniel Sazhin, multiple US National Champion, who was kind enough to brief me on soaring in Montague, CA and Nephi, UT – the sites of my first two soaring contests that I had registered for.

Then, as we all know too well, everything changed.  Much of the world went into lockdown.  The contests I had signed up for were cancelled.  And instead of soaring, I found myself drafting a Covid-19 policy for our club to help us get back in the air. After all, “social distancing” isn’t all that difficult in our sport.

Club operations resumed in early May.  And by the end of that month the OLC Speed League Season started with a five week delay.

Looking back at 2020, the soaring year turned out much better than expected. These were the goals that I had set for myself a year ago:

1. 1. Stay safe by always heeding my own advice.
   2. Move up to flapped gliders, fly with water ballast, and learn to responsibly use an engine.
   3. Have fun flying my first soaring contests (I’m signed up for the 2-seater Nationals in Montague, CA; and the Region 9 Sports Class in Nephi, UT). My goal is to complete all tasks provided that I can do so without taking any safety risks.
   4. Contribute to my club’s OLC Speed League results by scoring among the top three Boulder pilots on 10 or more Speed League weekends. My stretch goal for the OLC Speed League is to score among the top 5 Boulder pilots and among the top 50 US pilots overall.
   5. Complete a flight of more than 750km. My stretch goal is 1000km.

How did I do?

Despite the challenges we all faced, the soaring year 2020 turned out better than might have been expected.

Goal #1 – Stay safe.

This will always be my most important objective.  I’m glad to say I succeeded in staying safe.  However, I recall one situation where I pushed my luck further than I should have when I continued a particular flight under a rapidly over-developing sky.  This got me into a terrifying situation: I had to return across a line of thunderstorms with lightning flashing across my canopy.  While the outcome was benign, the experience was scary and not something I ever wish to repeat.  I have definitely been much more respectful of potential thunderstorms ever since. At some point I must find the courage to write about it in more detail so others can learn from it, too.

Goal #2 – Move up to flapped gliders, fly with water ballast, and learn to responsibly use an engine.

My new-to-me Ventus 2cxT allowed me to make good progress.  Most of my summer soaring flights were with different levels of water ballast. I am now quite comfortable flying with high(er) wing loadings.

Flying with flaps has been much less of a deal than I had imagined.  The flap controls in my Ventus are extraordinarily well designed.  The pilot’s hand can comfortably rest on the flap handle. Making adjustments is no effort at all. Working the flaps is as intuitive as working the elevator.

The integration of flaps and trim makes trim adjustments largely unnecessary.  Hard to beat that design!

I started the sustainer engine a few times for test purposes but I rarely ever used it to climb, and I never used it to self-retrieve, although once I came close.  You could say that’s a responsible use of the engine but I wish I had got to know it a bit better. There’s more opportunity for that next year.

Goal #3 – First Contests.

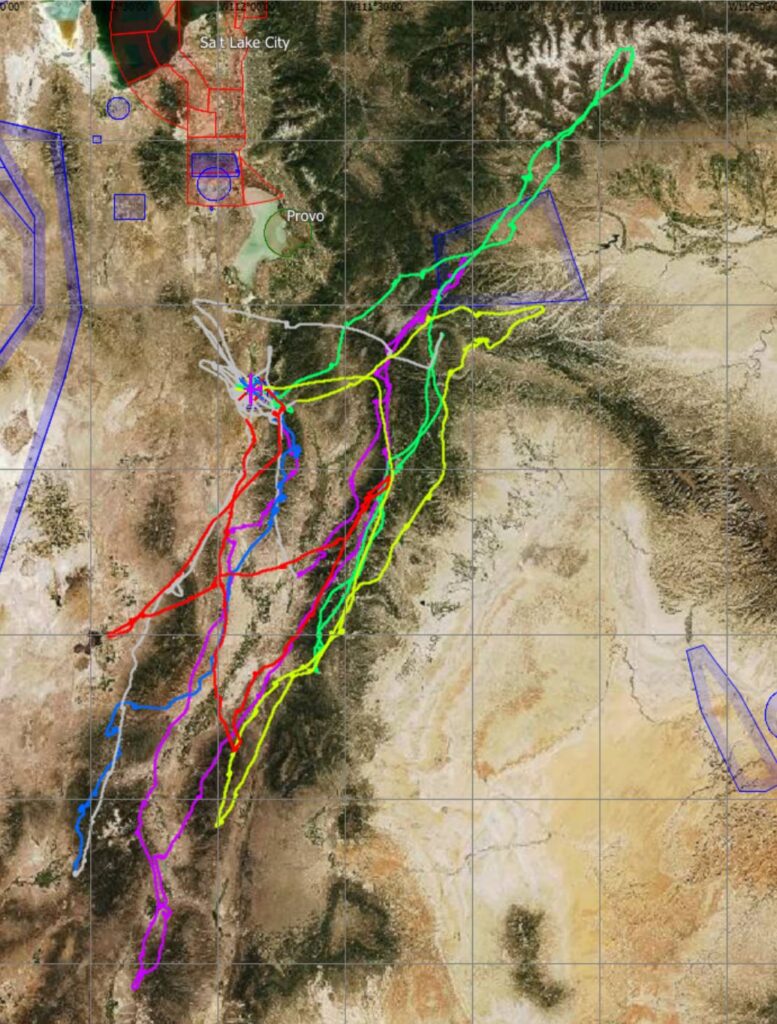
Almost all US contests were cancelled and moved to next year so this will remain one of my key objectives in 2021. To practice, I did manage to travel one week to Nephi to fly with Bruno Vassel and a number of other XC pilots.  The experience was invaluable as I was able to fly a number of good tasks and am now much more familiar with the terrain and the prevalent energy lines. This flight also provided a taste of what racing feels like.

Goal #4 – Contribute to my club’s OLC Speed League Results.

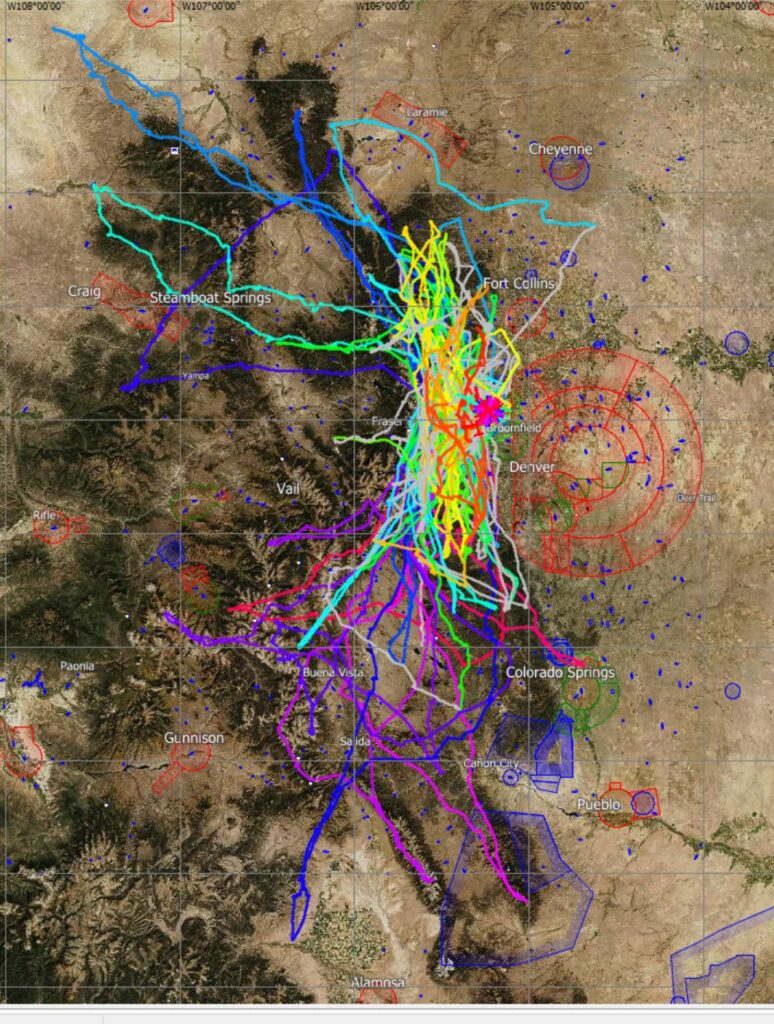
Boulder has had it’s best year ever competing in the speed league with a number 2 placement in the US Gold League and the World League.

My own contribution met my objective of placing among the top 3 Boulder pilots on more than half of the speed league weekends.  I learned a lot about flying faster and feel much better prepared for future XC flights.  I wrote more about my learnings from the Speed League in this article.

Among all Boulder pilots I over-achieved on what my stretch goal of scoring among the top 5 pilots overall by coming in 3rd place behind John Seaborn (a multiple national champion) and Bob Caldwell (one of Boulder’s most accomplished XC pilots). Among all US Speed League pilots I scored 25th, also well within my goal of landing among the top 50.

Goal #5 – Complete a flight of more than 750km.

It took me eight attempts but on August 7 I ultimately achieved my objective of completing a pre-declared 750km flight.

My longest flight of the year (per OLC rules) was 916 km.  I’m now inspired to reach for 1000 km if the conditions permit.

14er Challenge.

In addition to these goals I also made good progress on the 14er Challenge: flying over the peaks of all mountains in Colorado that are at least 14,000 ft tall. At the beginning of the year my tally stood at 11 out of the 58 peaks.

In 2020 I succeeded in “bagging” another 28: the fifteen 14ers of the Sawatch Range, the seven 14ers of the Elk Range,  and five of the ten 14ers in the Sangre de Cristo Range.  I also flew over Mt. Bross, my last missing peak in the Mosquito Range.

My overall tally is now at 39 with another 19 peaks to go: the five southern-most peaks in the Sangre de Cristo Range, and all 14 peaks in the furthest-away San Juan Mountains.

Total XC Distance.

In 2020, I flew a distance of 19,728 km (based on OLC plus rules using a maximum of 6 legs per flight), almost half-way around the earth, at an average speed of 116 kph.

In my next post I will try to set new goals for 2021.

We all know pilots who fall into one of two buckets. Bucket 1 contains pilots who never leave glide range around their home airport. Bucket 2 contains pilots who don’t seem to hesitate at all before they venture out over completely unfamiliar terrain.

Bucket 1 pilots don’t know what they’re missing. Bucket 2 pilots don’t know what they are doing. The former will die of old age but with regrets in their hearts.  The latter might not get that far…

These two groups tend not to have too much in common except for one thing: they don’t know their turf. The first group because they don’t need to. The second group because they think they don’t need to.

And then there is a third bucket: it contains those who confidently leave glide range of their home airport, push their boundaries, and do so responsibly. These are pilots who want to live to old age and without regrets.

This article is for those who want to become a Bucket 3 pilot.  How can you join? Get to know your turf!

The place I fly from – Boulder, Colorado – is an extreme case in point. The terrain is unforgiving: there are mountains, canyons, woods, and rocks.  Boulder was given its name for a reason.  Except for airports that are often 40 or 50 miles apart there are few places to land.  And even some of the airports have runways too narrow to put a glider down.

What about the prairie? Yes, we do have a flat prairie to the east of the mountains.  But it is rarely a good place to soar and the best lift is almost always over the mountains.

A basic rule of thumb for our area:  where you can land you can’t soar, and where you can soar you can’t land. (This is a bit exaggerated but you get the point.)

It is no wonder that our club has many Bucket 1 pilots who always stay within easy glide range of our airport.  Bucket 2 pilots are rare and a temporary exception: they tend to figure out quickly how get to Bucket 3 or they would not last very long. We also have many pilots who successfully graduated into Bucket 3.  It is these Bucket 3 pilots that make the Soaring Society of Boulder one of the most successful cross-country soaring clubs – not just in the US, but in the world.

If you have been a Bucket 1 pilot (wherever you fly) but want to join Bucket 3, what do you have to do and how long does it take?

Are You Ready to Become a “Bucket 3” Pilot?

Let’s acknowledge that you should have some basic competencies as a soaring pilot before you venture further afield.  E.g., you should be able to read the soaring weather forecast, tell the difference between a developing and a decaying cloud, center a thermal and don’t lose it. On a good soaring day you should have no difficulty staying aloft, and you should be able to confidently move from thermal to thermal.  Some pilots (usually younger ones) learn to get there within one or two seasons and about 50-100 hours of flying. Others may need a bit longer.

Three years ago, at the end of my first season flying from Boulder, I was one of those Bucket 1 pilots, eager and ready to figure out how to get to bucket 3.  My logbook at the time showed a total of 200 flights and 100 hours of soaring as pilot in command. 70 flights and 60 hours were in that one season; the rest dated back to my teenage years in the 1980s. All my flights up to that point had been local, i.e. within easy glide range of the takeoff airport.

What It Means To Know Your Turf

Cutting the cord to get back to your home airport is a huge milestone for any soaring pilot, second only to their first solo flight. It can also feel very intimidating. But you can remove a lot of the trepidations if you know what you are doing.

This means: be prepared before you venture off into the unknown!  You have to know the terrain that lies ahead and where you might find lift (or sink).  Most important of all: you must know exactly where you can land if the expected lift does not materialize.

Knowing where to land, how to ensure that you can always get there, and where you are most likely to find lift is at the very core of what it means to know your turf!

How To Learn Your Turf?

If you are new to cross-country soaring, chances are that you have some homework to do.  The same steps apply before you fly in an unfamiliar area.  As you gain experience you will become quite efficient in your learning process but that does not mean that should ever skip any of the following steps:

• 1. Research viable landing sites
  2. Understand how high you need to be wherever you fly
  3. Familiarize yourself with typical energy lines (i.e. where to find lift)

Each of these three steps is discussed below.

My recommendation is that you select the most suitable soaring area beyond your home field’s glide range.  Let’s call it your Task Area.   Then you complete the three steps before pushing your boundaries further.  Keep your initial Task Area reasonably small – otherwise you might become overwhelmed and give up before you even make your first cross-country attempt.   Expand your turf one step at a time!

E.g., for pilots flying from Boulder, Colorado, it may be best to initially concentrate on the area east of the Front Range between I-70 and the Wyoming border.  This area is easily accessible, offers excellent soaring conditions, and provides access to several landable airports.  Only when you are completely familiar with this particular area, i.e., if you know your turf, does it make sense to research additional – and more demanding – areas to the south, west, and north, and north-east.

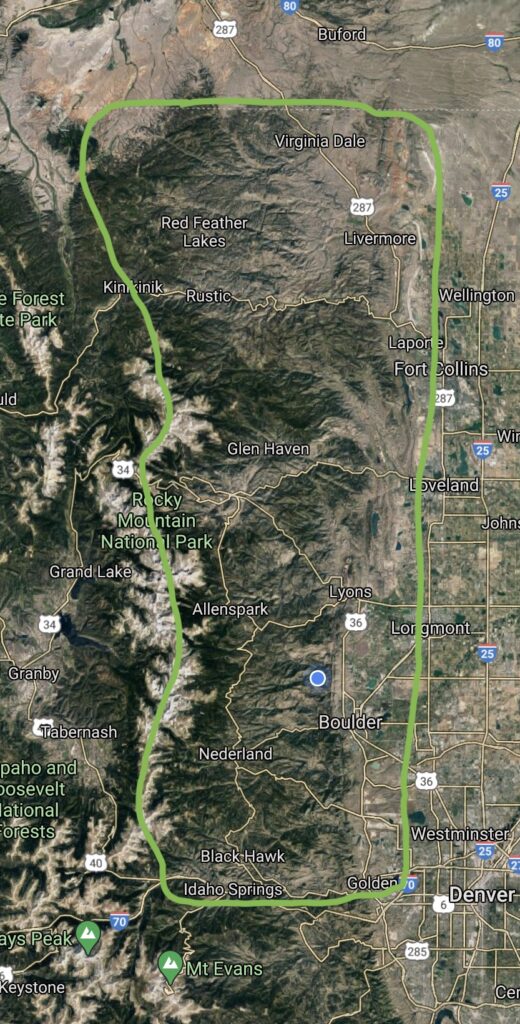
If you don’t already know what the best area is for your first cross-country missions, I suggest you ask the more experienced pilots at your soaring site.  You want to select a task area that best meets the criteria just described.

1. Research Viable Landing Sites

Assuming you have prioritized and selected a task area for your first cross-country flights the first thing to do is to research where you can safely land.

a) Select suitable airports in your task area

Airports in your task area are easy to identify with the help of a sectional map (or an online version thereof – e.g. skyvector.com).  Most will also be marked on the local waypoint database that you can find on the Global Turnpoint Exchange.

However, not every airport is suitable for landing a glider, or for your glider in particular.

Towered airports tend to have big and wide runways but they are not glider friendly.   I don’t like the stress of approaching a busy airport and explaining to a controller (who may know very little about gliders) why I am unable to stay in a holding pattern and need to land immediately.  I will use such an airport if I have to, but it’s not something I would recommend to anyone on their first cross-country flights.

Smaller public airports are usually the best choice but you have to know how wide the runways are and if the width will be sufficient for the wingspan of your ship.  A 60 foot-wide runway may or may not be sufficient for an 18 meter (59 ft span) glider: you also need to know if there are runway lights and whether they are immediately at the runway’s edge or located several feet to either side.   If you zoom into satellite images on Google Earth you can usually see the lights.  You can then use the online measuring tool to check the distance between them.

Private airports can also be acceptable choices but you need to be extra careful during your homework.  Often they are built and maintained for bush planes with high wings and narrow spans.  The terrain may be too uneven for the long and low-hanging wings of a glider, or the ground may be rising next to the edge of a narrow runway.

Online research is a good way to check them out but be very careful not to overlook anything! You can also never be certain that there aren’t any new obstacles when you turn up on final approach: e.g., there may be tall vegetation next to the runway that wasn’t there when the satellite image was taken.  A fence may have been erected.  Or a huge bison, a vehicle, playing children, or some other unexpected obstacle may appear in the middle of the runway when you arrive. If you land there, most private owners are likely to be welcoming but you may also find the owner absent and your retrieve crew stuck behind locked gates a long driveway away.

Under no circumstances should you trust that private airfields marked on the sectional map or on the waypoint file are suitable.  They might not even exist anymore and were just never removed from the map (or the waypoint file)!

Public airports are generally the best choice for landing out because they tend to present fewer surprises.  If the runway is long, smooth, and wide enough for an aero-tow take-off they may also offer the extra conveniences of an aero-retrieve.

b) Where to look for suitable land-out fields

In areas where suitable airports are far apart of poorly located relative to the best soaring conditions, land-out fields can offer a safe alternative.

In some soaring areas fields are large and plentiful.  E.g., driving through Texas I noticed that many fields are bigger than most airports and much of the area is as flat as a pancake.  At certain times of the year you can land practically anywhere.  Land-out Mecca!

However, if your soaring area looks more like Colorado than Texas, it pays to be strategic and ask: are there suitable landout fields where you might need them the most? Here are some prime examples:

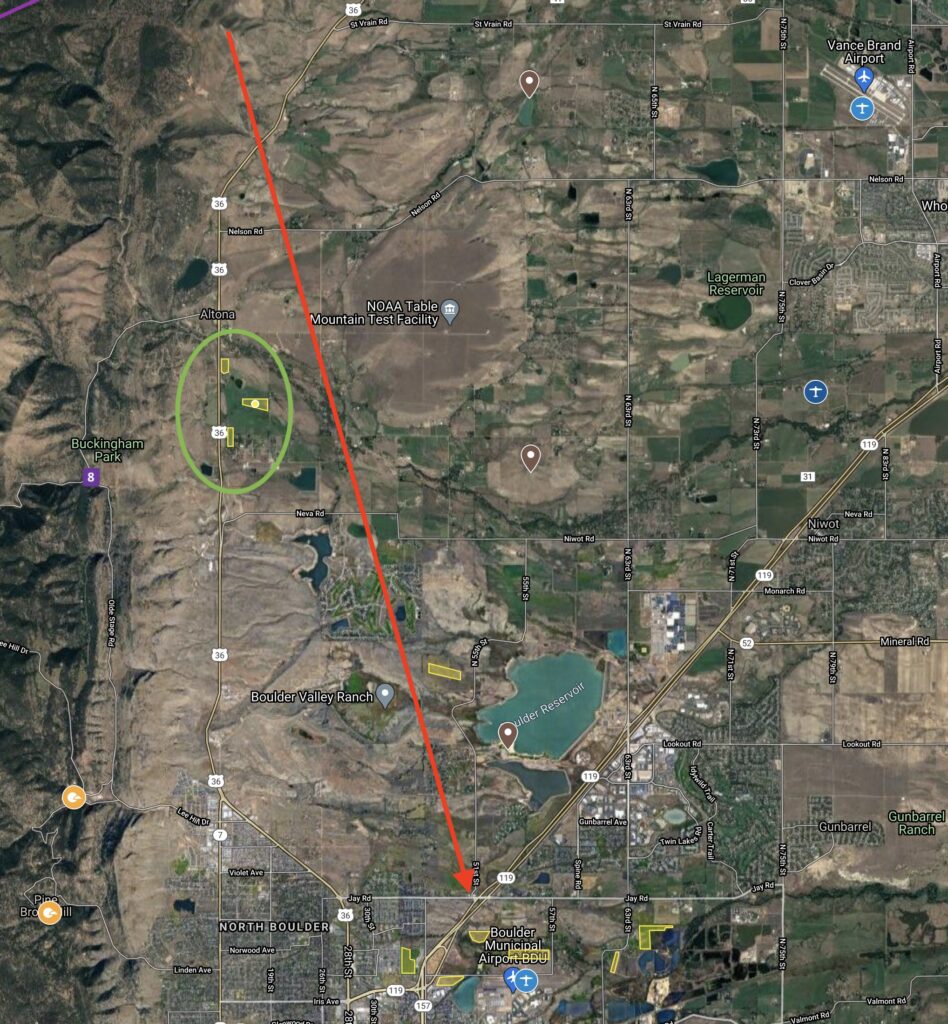
Along your final glide path: a common scenario is that you return from a cross country flight at a time of day when the lift is dying.   If you are low and hit unexpected sink after you’ve passed the last airport on route, where would you land?  E.g., for those flying north from Boulder it is worth researching specific fields between Lyons and Boulder when Vance Brand airport is no longer an option.

Along the base of the hills and in the valleys: soaring pilots normally fly over the hills and mountains because that’s where the lift tends to be best.  If our strategy is to always stay within glide range of a suitable airport, we may be forced to quit searching for lift over the hills and fly out into the plains to an airport while we are still quite high.  This means that having to land at that airport becomes very likely because it is usually much harder to find lift over the plains than over the hills.  However, if we positively know where we can safely land right at the base of the hills without necessarily having to reach an airport we can continue to search for lift over the hills, thereby greatly increasing the odds of avoiding a landout altogether.

Before major terrain obstacles:  if there are terrain obstacles along your flight path be prepared for the possibility of not being able to clear them.  A prime example for Boulder pilots is the northeast corner of South Park: Mount Evans is a big terrain obstacles for pilots returning from the southwest and if pilots fail to find lift to get over the mountains they must know the fields where they can safely land.

Across hostile terrain: glider pilots tend to fly along the same flight paths again and again because energy lines tend to set up in the same places (see chapter 4 below). If such flight paths include long stretches over largely unlandable terrain (e.g. undulating hills, big forested areas, etc) it can be vital to know the precise location of the few places where a somewhat safe landing may be possible.

E.g., for Boulder pilots flying towards Wyoming one such stretch is between Estes Park and the Laramie valley: 50+ miles of mountains, woods, rocks, and canyons with the nearest suitable airport often 30+ miles away. The only (private) airstrip at Crystal Lakes is too narrow for gliders but it is worth knowing the exact location of the only two meadows where an emergency landing might be possible.

c) How to Research Specific Landout Fields

After deciding where to look for fields you need to do the work of identifying and verifying them.  If you are confident about a specific field in a strategic area you should load it into the waypoint database on your flight computer. This is the best way to quickly locate the field when you’re flying.

Starting Point: a good place to start is the Worldwide Turnpoint Exchange.  Locate the waypoint file for your area and view it with your flight planning software or in Google Earth.  Waypoint files are likely to include some landout fields. Just know that these were put together by volunteers, often many years ago, and you must never rely on them.  They are just a starting point for your own research!

Satellite Maps:  the next step in your research is to examine satellite imagery on Google Earth or Google Maps.  Familiarize yourself with the 3-D view and the use of the distance measuring tool.  If you locate a potential field in a strategic area, try to glean as much information as possible from the satellite image.

• • View the field from all sides in 3-D view to identify any slope. If a slope is visually noticeable the field will almost certainly be unusable.
  • Next, measure the length and the width of the field with the online measuring tool.  Then zoom in and carefully examine the surface: is it possible to tell what kind of field it is?
  • Can you spot farm animals?  Look for any visible rocks, buildings, ditches, irrigation equipment, or other ground obstacles.  Demarcation lines across the field (e.g. indicated by different shades of color) could suggest a fence which will not be visible from the satellite image.
  • Also check for power lines in the area (these may be impossible to detect but shadows sometimes give them away).  If there is a road next to the field, assume that a power line may run along the road.
  • If there are prevailing winds in the area consider what impact they are likely to have on the landing direction.
  • Imagine how you would fly an approach into the field to identify any terrain or approach obstacles.
  • Finally, examine the road access.  If a field looks good but seems inaccessible for a glider trailer it may just be of use in an emergency.

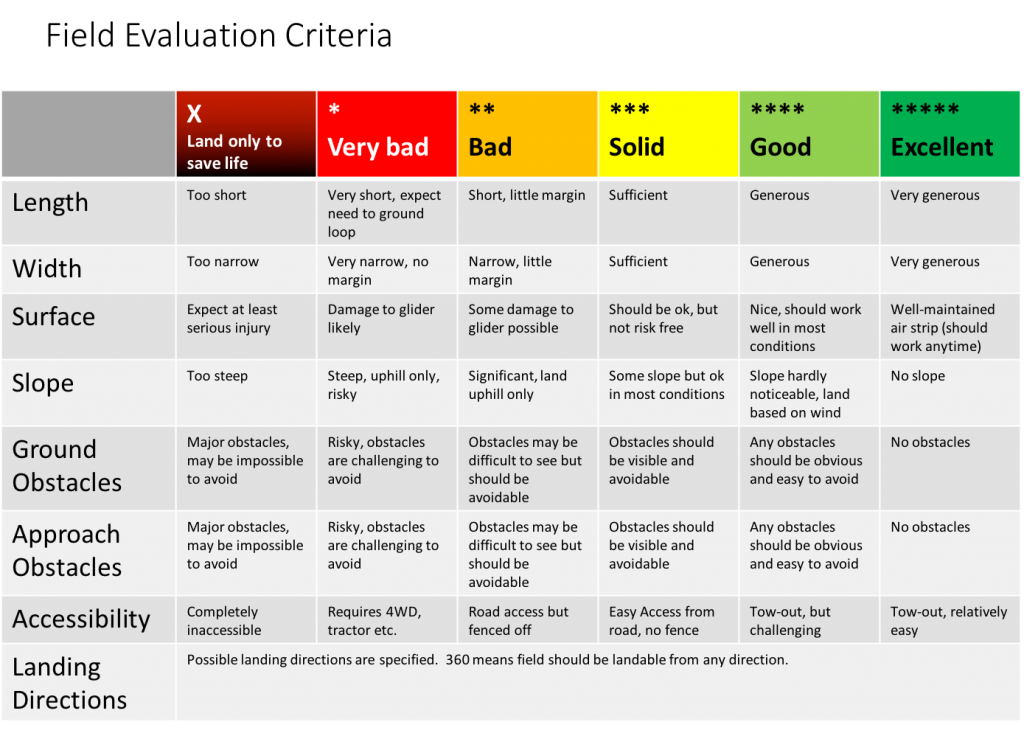
If you like a field and think it is worthy of further examination, try to do a preliminary evaluation and take notes of anything that may be of concern.  I note the GPS coordinates for each potentially viable field and make some initial evaluative guesstimates on a 5-point scale for each of the following characteristics: length, width, slope, surface, potential ground obstacles, approach obstacles, and road access.

I also note potential landing directions. If a field has some clear deficiency I may classify it as “emergency only”.  When I later visit a field on the ground I revise my initial evaluation – this process can be eye opening because the reality always looks different than the satellite image.

Examining the first few fields using this method will take a while but you’ll quickly get better at it. Note, however, that you can never positively identify a field as suitable just from an online review!

Visit and Verify: the only way to get reasonably confident about the suitability of a field is by visiting it.

There are two good ways to do so. The most thorough one is to visit the field on the ground.  Ideally you would want to walk around in the field but doing so may involve trespassing and attract unwanted attention.  But even just stopping next to the field and looking at it from the road will tell you a lot of things you might have missed.

Small to medium-sized rocks, uneven terrain, fences, ditches, or power lines are typical examples.  You might find out that the farmer is now growing tall crops in what previously looked like a hay field. You may find the field full of cattle. You may even find that there is no longer a field at all but a new housing development or a gravel pit..

Visiting fields makes you appreciate the static nature of a satellite image and is a powerful reminder for why you must not blindly trust your online research!

A good alternative (or complement) is to visit fields by air with a touring motor glider or a small power plane.  You might not be able to see everything as well as during a ground visit but you will gain another invaluable perspective: you can fly low approaches into the selected field with the engine idling and then go around.  It is easy to imagine what the approach would feel like in a glider.  Touring Motor Gliders are particularly well-suited for this endeavor.  Another advantage of this methodology is that you can see many fields within just one or two hours whereas a road trip to visit the same fields on the ground might take one or two entire days.

Can you not also examine fields from your regular glider the next time you fly over the same area? Well, you can identify where they are (and you should do that) but you will normally not be able to get close enough to learn much more than what you can learn from viewing satellite images. In Colorado, where we typically fly many thousand feet above the ground, almost every mountain meadow looks easily landable until you get low and close and it becomes obvious that you’d be lucky to survive if you had to put your glider in the middle of it.

Whether you do ground visits, air visits, or both, you should also familiarize yourself with the typical crops and their growing season in your area: what is being grown? how tall does it get? when is it harvested? is the ground soft or firm? In other words: which of the fields will be (most) suitable to land in at the time of your flight and how do you recognize suitable fields from the air? This is even more important if you do your ground visits in the off-season.  Fields look vastly different in winter than during the peak soaring season.  You should also research the types of irrigation systems being used (if any) and how you can avoid them.  Most irrigation systems will not stop when a glider shows up in the field and the machinery might just roll over it.

d) Practice With Condor

This isn’t a necessary step but it is super useful and fun.  If you have access to the Condor Soaring Simulator and there is a scenery for your soaring area, you can practice landing in your chosen fields.  This has multiple key benefits:

(1)  You become familiar with the visual view of the most hostile terrain from “down low” – a perspective that you hope to never see in real life.

(2) You experience what it would be like to land in the fields you have selected, and you test the approaches with different gliders and under different wind conditions.  If you ever have to use one of them, you’ll be better prepared and know what to do.

(3) You can repeat this exercise over and over again at no risk to you or your glider until you feel confident that you would not screw it up.

(4) You gain valuable practice for how to land in small fields – how to judge your altitude above ground, how to control your airspeed and glide path, how to clear obstacles, how to deal with cross winds and turbulence, and how to touch down with minimal energy.

These skills come in handy for all your future real-life landings and are invaluable if you have to put your glider into any small field.

If you do practice with Condor, remember to never use it for the purpose of field selection!  Condor will allow you to land in lots of places that are not at all landable in real life!   You must select your fields in real life and use Condor only for landing practice!

Here is a video recording of a Condor flight to a number of emergency-only fields in the foothills of the Rocky Mountains. This shows you how to use this tool.  It is a lot of fun!

2. Understand How High You Need to be Wherever You Fly

One of the most fundamental safety rules in soaring is to always keep an airport or some other suitable landing site within safe glide distance.

However, applying this simple rule isn’t always easy.

a) Benefits and Challenges of Relying on Your Flight Computer

When you’re flying, the easiest method is to use the final glide calculator of your flight computer.

E.g., if set up to do so, my Oudie flight computer will display the expected arrival altitude above a specific airport or landout field if flying at the selected McCready setting (MC).

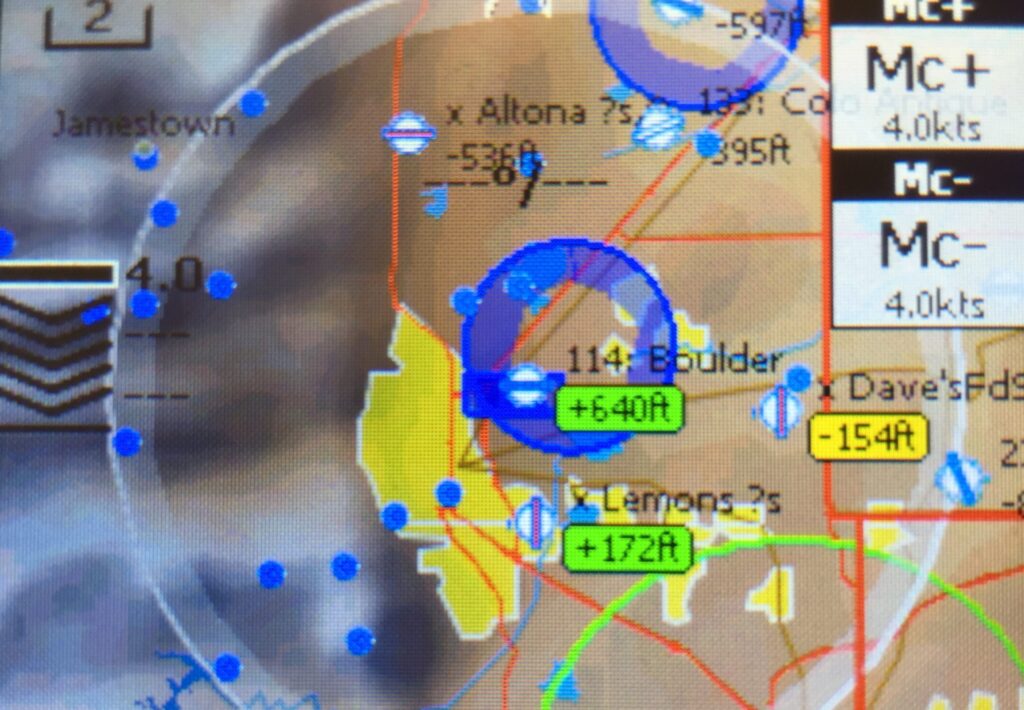
This works pretty well assuming that you selected the correct polar for your glider, that you accurately entered the weight of the pilot and water ballast, that you used reasonable bug settings, that you set an appropriate safe arrival altitude, and that you fly in accordance with MC.  It also assumes that there is no vertical air movement along your flight path, especially no unexpected and prolonged sink.

It took me about an entire soaring season to learn to trust my flight computer.  This has a lot to do with the fact that I did not trust myself to program it correctly.  Remember the standard rule for any analysis or machine output: if you put garbage in, garbage comes out!

I also learned to appreciate the impact of different MC settings (a higher setting gives you some extra safety margin because you can conserve energy by slowing down), and the significance of lift or sink along the way.  One of my more memorable learning experiences in this regard was on this long and somewhat exciting final glide.

Anyway, there are a lot of reasons for why I do not recommend that you simply trust the flight computer on your first cross-country flights!

b) Create Your Own Glide Map with Glide Rings

I recommend you use the off-season to study maps and determine for each part of your chosen task area how high you need to be to safely reach the next safe landing area.

How do you do that? You probably learned a simple and reliable method as part of your initial flight training: you take a map of your task area, mark the chosen airports and any personally verified landing fields, and then use a pair of compasses to draw concentric circles around each chosen landing site.  Each ring should indicate the minimum altitude that you need to be at in order to glide to the landing site and arrive there at a safe pattern altitude.

First, you pick a safe pattern altitude.  I recommend at least 1500 ft, especially for airports or fields where you have not landed recently.  For busy airports you may want to add some additional margin.

Then you pick a conservative glide ratio that is appropriate for “sinky” conditions.  Since you’re doing this exercise in the off season, you don’t know what the weather will be like on the day you’ll be flying, so err on the safe side.  I have encountered 10+kt sink for stretches of five miles or even more.  What’s conservative also depends on your soaring area.  This excellent booklet on mountain flying recommends to use half of your glider’s best glide ratio. In benign conditions this will feel overly conservative. In extreme conditions it may not be conservative enough! You may also want to discuss this with your flight instructor.

For Boulder I have created such a map with the help of Glideplan, a special piece of software that I bought for this purpose.  Note that this map is designed for high performance gliders and assumes a glide ratio of 1:27. It may thus not be as conservative as you want it to be!

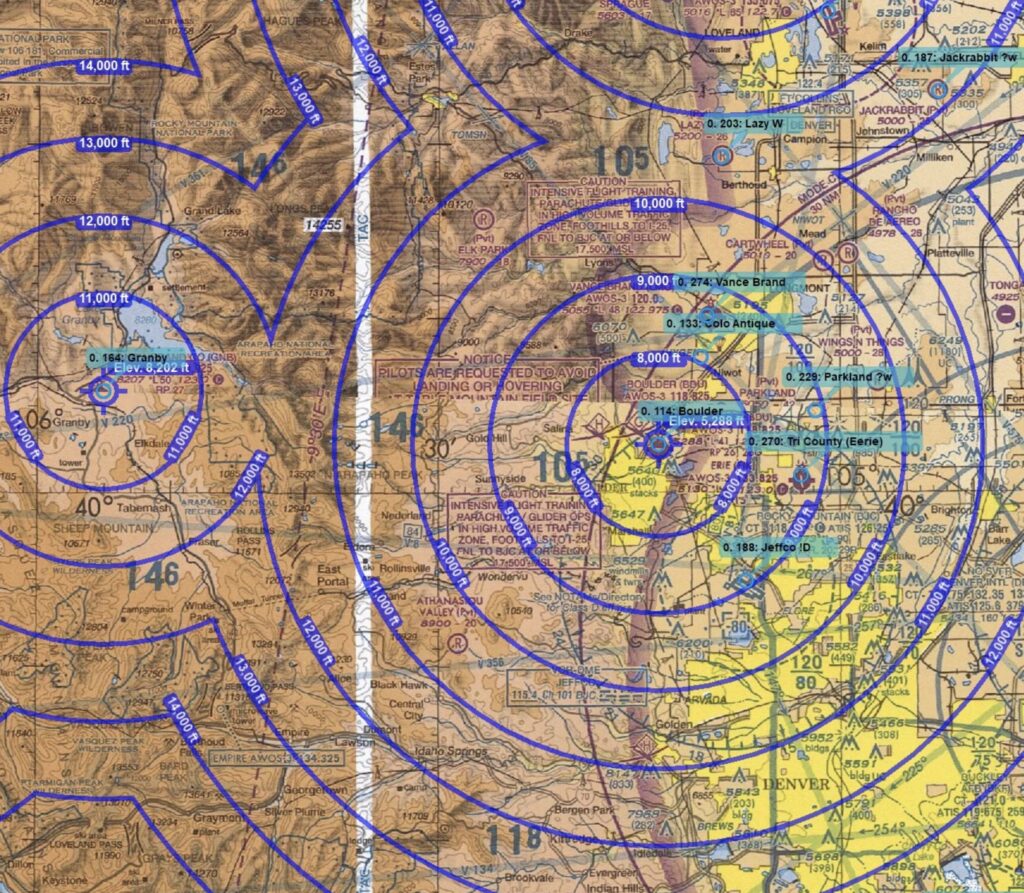
Glideplan is just a tool that facilitates the drawing of such circles on top of a current Sectional Chart but you can easily accomplish the same thing manually, using the process described above.  One advantage of doing this by hand is that you will better remember the information when you’re flying.  You can of course put a physical map with glide rings into your cockpit but I personally found it quite challenging to use during flight, especially when you are already relatively low and your workload is pretty high.

c) Account for Terrain Obstacles

Whether you create your glide map with glide rings, use a software to do so, or rely primarily on your glide computer: make sure you account for terrain obstacles that may lie between you and your nearest landing site(s).

Some glide computers such as the LX 9000, ClearNav, or even open source software such as TopHat and XC Soar will help you with this by displaying a “glide amoeba” on your screen.  This will show if your glide path is blocked by a mountain, hill, or ridge line.  Other computers such as the Oudie do not offer such a feature.

Whether you have such a computer or not, you should study the potential terrain obstacles that may exist in your task area and account for this by adjusting your personal glide map so that you positively know how high you need to be at any given point to clear any obstacles that may exist.  To do so, just use a safe minimum clearance altitude for your obstacles (e.g. 500-1000 ft) and then apply the same conservative glide ratio from there.

For pilots flying from Boulder, here is a brief list of some of the terrain obstacles nearby:

• • Flatirons – do not get low on the west side of the Flatirons.  Your only escape route may be through Eldorado Canyon and chances are that you will not make it back to Boulder.
  • Thorodin Mountain and Black Hawk – do not get trapped on the west side of Thorodin Mountain.  Your glide computer may show Boulder airport in glide but chances are that you’re not. There are no safe landing options in that area. You may not even be able to glide out to one of the (poor) fields near Golden.
  • High terrain east of Estes Park – if you get low in the Estes Valley, you will get trapped by the hills to the east. The landing options in Estes Park are marginal at best.  This flight got me to contemplate my options.
  • The Rampart Range.  This is a ridge line along the southern foothills roughly between Twin Ceders (south of Conifer) and Woodland Park (northwest of Colorado Springs).  Good lift can often be found along the convergence several miles west of the Rampart Range (e.g. near Cheesman Lake).  However, be careful not to get trapped over completely hostile terrain between the Rampart Range and the Terryall Mountains (the ridge line along the eastern edge of South Park) to the west. Your computer may show the private airfield of Perry Park in glide but there is no way to get there. Before you know it, ditching your glider in the lake could become the safest of all the unpleasant options.   On my first flight over Pikes Peak I dropped to 12,700 ft, uncomfortably low for in this area.

3. Familiarize Yourself With Typical Energy Lines

Following the advice in sections 1. and 2. above should help you stay safe during your first cross-country flights. This last section will help you find the most common lift lines within your task area.

It’s easy to see why that’s important: following lift lines makes it much easier to go places and you’re also more likely able to stay high and avoid having to put your land-out knowledge to an early test. After all, wouldn’t it be great if your first XC flights were successful and free of land-out-stress?

Most soaring areas have typical recurring weather patterns. For each weather situation, lift lines tend to set up in roughly the same places again and again.  This is especially true for mountain sites where ridge lift, convergence lift, and wave lift are a function of topography and wind. Many mountain sites also benefit from valley breeze, mainly a function of topography and sun angle. Thermals almost always set up first over the high ground where they are also stronger (albeit often narrower).

You will be able to obtain a wealth of information by talking to experienced cross country pilots at your site who are often eager to share their exploits.  Quiz them about what lines they fly most often in the most common weather and wind patterns, and what causes the more typical energy lines to set up.

Another way to find out is to download flight traces from flight sharing sites such as OLC (Online Contest).  Pick the better traces of pilots who are know to fly the longest and fastest tasks at your specific site.  Also, if competitions were held in your area, it is useful to download the flight traces from contest tasks.

Once you have found and downloaded such traces (20-50 traces is a good number to start), load them all into a flight analysis software such as SeeYou and overlay them on a single screen.   (OLC limits your download to 20 flights per day, so just stick with it over a number of days.) Chances are that the patterns will jump right out at you.

If you can see where pilots fly most frequently you still want to understand why they tend to find lift along the same lines.  The answers are likely very specific to your site and once again it is best to quiz these pilots directly.

In Boulder, by far the largest number of XC flights follows the convergence line that normally sets up over the foothills east of the Continental Divide and runs parallel to the mountains.  I have written multiple times about it.  Getting to the line is not always easy, but once you have learned to recognize and follow it, the rewards are amazing.  Understanding the convergence is really critical for local XC pilots. On strong convergence days it can be close to impossible to complete a successful XC flight if you’re to the east of the convergence.   It can be very frustrating for those who did not make it into the convergence to look at the amazing flights of those who did.  On the other hand, convergence days offer fantastic opportunities for badge flight such as my first diamond goal flight.

As an example of what you can learn from contest flights, take a look at this analysis that I completed in preparation for a contest in Montague, California.  The typical flight patterns are easy to see.  Conversations with pilots who previously competed there helped me understand the energy lines.

Bringing It All Together

“Bucket 3 pilots” don’t stay stuck in glide range around their home airport but neither do they head out blindly over unfamiliar and potentially hostile terrain.  Instead, they have done their homework.  They selected an appropriate task area. They know where they can land safely. For each part of their task area they understand how high they have to be to clear terrain obstacles and reach safe landing sites. They also understand the typical energy lines that tend to set up in their task area.  In other words: they know their turf.

By becoming a bucket 3 pilot you drastically increase your chances that your first cross-country flights will be successful, safe, and less stressful.

Boulder pilots can take a look at my personal Boulder Soaring Area Map where I have documented the results of my own research.  Instructions for interpreting and using this map can be found here. This is and will always remain a “work in progress”.  I have visited many fields on the ground, especially along the Front Range and across South Park.  An evaluation of fields along the Northern Front Range dating back to 2017 can be found here.

However, remember that such visits are just a snapshot in time based on what I could observe on the specific day of my visit. Our environment obviously continues to evolve.

Given the size of the covered task area, it would also be impractical to visit all the potential landing sites in person. If I am not certain about a field, I will only treat it as an “emergency site:” good enough to minimize physical harm to myself but not to my glider.  As a rule, I keep at least one good airport or a positively known landable site in glide at all times. I will only fly over “emergency-only terrain” when I am certain that I there is a line of good lift along the way.

If this seems like too much work remember to limit your initial task area!  Your first XC flights won’t lead you all across your state or even into neighboring states.  By selecting an appropriate and realistic task area for your first cross-country flights you can drastically reduce the scope of the required homework.  One or two weekends of online research, a few phone calls with experienced XC pilots at your soaring site, plus a day or two of visiting fields on the ground (or a flight in a touring motor glider) should give you plenty of information.

If that still feels like too much work there’s nothing wrong if you keep floating around your home airport!  After all, it’s your hobby and our choice what you make of it.  Just don’t succumb to the temptation of heading out into the hostile unknown!

However, if you have read all the way to the end, you must have what it takes to become a Bucket 3 pilot.  Have fun getting to know your turf!  I wish you great success on your upcoming cross-country missions.

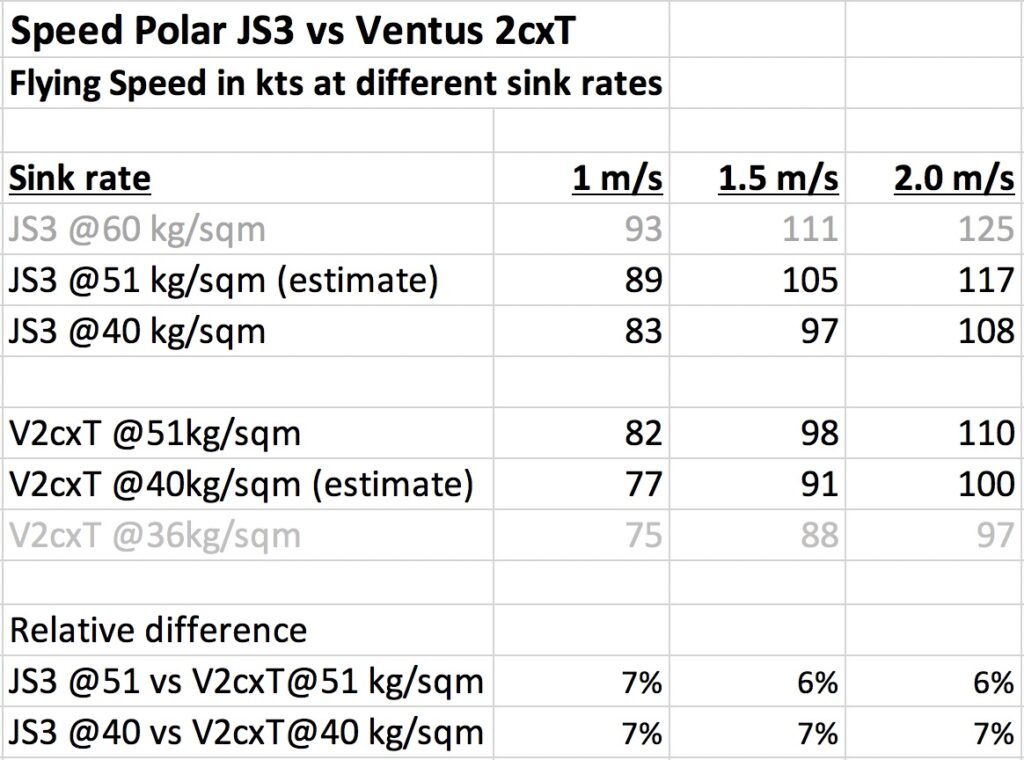
Note: in the initial publication of this article I made a mistake when extracting data points from the JS3 polar curve.  Thanks to Matthew Scutter for pointing this out to me.  This error has been corrected below.

The published performance data from Jonkers Sailplanes and Schempp-Hirth, suggest a very significant performance advantages of the JS3 over the Ventus 2cxT.

The data suggest that a ballasted JS 3 flies 12% faster than a ballasted Ventus 2cT at a wing-loading of 51 kg/sqm.  Unballasted, the JS3 is shown to be 9-10% faster than an unballasted Ventus 2cxT.  (All data shown are for 18m configuration.)

However, one complication is that ballasted (or unballasted) the wing loading for the two gliders is different.

Let’s try to create a more “apples to apples” comparison by comparing the published performance figures at equal wing loading.  To do that we have to estimate the values for the JS3 at a wing loading of 51kg/sqm and that of the Ventus 2cxT at 40kg/sqm.  (To create the estimate I assumed that the attainable speed at a given sink rate for each of the gliders increases linearly with additional wing loading.  This methodology is probably not exactly accurate but any other plausible method would yield almost identical results.)

The table shows that even at equal wing loading the polar data still suggest a performance difference of 6-7% for the JS3.

[Side Note: per the manufacturer flight manual my Ventus 2cxT has a maximum all-up mass of 600kg (1323 lb) and is not limited to 565kg (1246 lb) as the polar curve suggests.  I.e., the maximum permissible wing loading is 54.4 kg/sqm and not just 51 kg/sqm. ]

Do those data points hold up in reality?

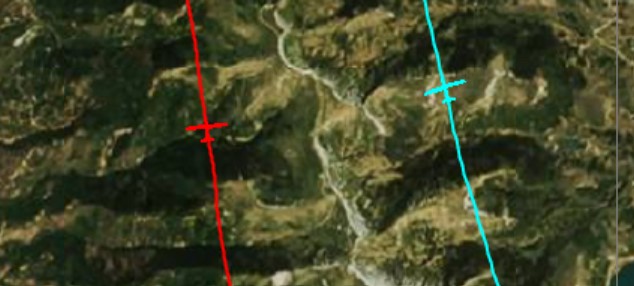
A little while ago I wrote about a Practice Race Day in Nephi on July 1.  One aspect that I did not give much attention was the difference in glider performance between John Seaborn’s JS3 and my Ventus 2cxT.  John and I flew the last 92.7 km (57.6 miles) within just three minutes of each other, which makes the results directly comparable.

I took a closer look at our flight traces to see how well my Ventus 2cxT held up against John’s JS3.  As a multiple National Champion John is unquestionably the better pilot, so we should expect John’s final glide to be at least 6-7% faster than mine if the published glider performance data are true AND if we flew with identical wing loading. (Both of us flew with 18 meter configurations.)

I was flying with approx. 80 liter of water ballast that day, which means my wing loading was right around 10 lbs/sqft (49 kg/sqm), very close to the 51 kg/sqm that Schempp-Hirth uses for their published polar curve.

I do not know how much ballast John had on board (although I do know that he flew with water that day) but I think it is likely that his JS3 was at or close to maximum gross weight, which would mean a wing loading of more than 12 lbs/sqft (close to 60 kg/sqm).  At full wingloading his JS3 should be about 12% faster than my Ventus. 

Is this true?  Let’s see!

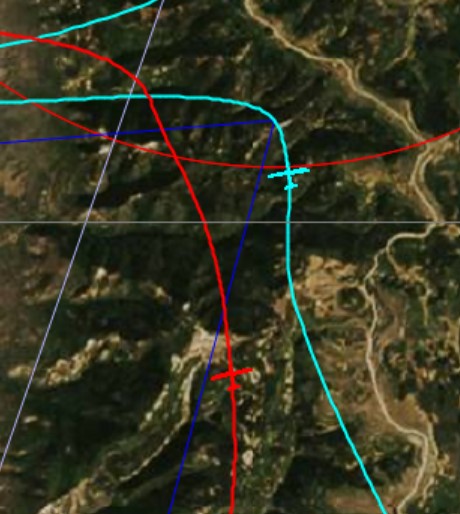
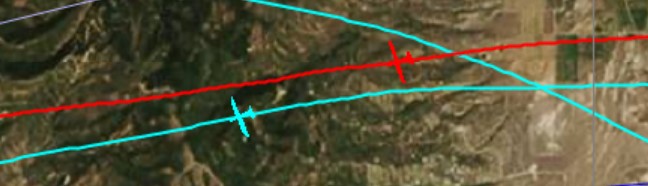
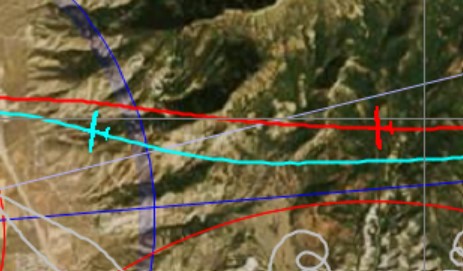
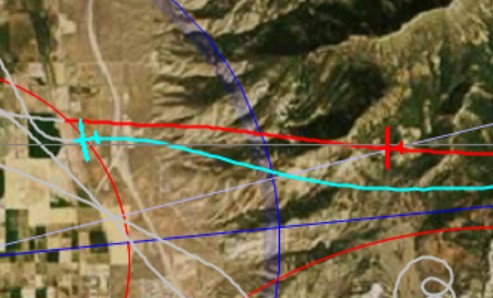
My flight trace is shown in red, and John’s is shown in blue.  Note that at this “starting point” John was exactly 3:00 minutes behind me.  My red glider is shown at 16:11:41 local time.  John reached the same spot (the location of his blue glider) at 16:14:41 local time.

What makes this flight so comparable is that we reached this location not only within 3 minutes of one another but also almost exactly at the same altitude.  In fact, I was at 16,428 ft MSL and John was at 16,508 ft, i.e., only 82 feet higher.

Let’s take a look at our positions exactly 5 minutes later.  I.e., my location as shown is at 16:16:41, and John’s position is shown exactly three minutes later, at 16:19:41.

We’re still neck to neck although John took a slightly more easterly line.  John also flew a little faster than me during his cruise, thereby losing more altitude, and decided to make two extra circles in good lift (where he gained 700 feet of altitude).  At 16:19:41 he was 270 degrees into his first circle.  My altitude was 16,672 and John’s was 16,494.  I.e., I was now 178 ft higher than John.

Let’s wind the clock forward another five minutes, i.e. 10 minutes into the glide):

There is still hardly any visible difference in terms of our location.  Since the prior position I had taken one pointless turn which netted absolutely no change in altitude.  John’s 700 ft altitude gain in his two circles is now reflected in a positive altitude difference between our gliders of 675 ft: I am at 15,639 ft and John is at 16,314 ft.

Purists may say that the true final glide only starts here since neither of us stopped to climb from this position until the finish.

Let’s jump ahead another five minutes. We’re now 15 minutes into the glide:

John took advantage of his positive altitude difference and flew significantly faster than I did.  He is now almost exactly 2 miles (3.2 km) ahead of me and about to enter the final turn point.  At our flying speeds this means that John is now almost exactly one minute ahead.  However, John’s higher speed came at the price of 1000 ft of additional altitude lost over the past five minutes: while he was previously 675 higher, he is now 371 ft lower.  I’m now at 14,697 and John is at 14,326.

Once, again, let’s jump another five minutes ahead.  We’re now 20 minutes into the glide:

John is still approx. 2 miles ahead.  I have put the nose down with the finish in sight and am more rapidly losing altitude.  At such very high speeds there is a steep price to pay for flying with less than maximum wing loading.  I am now at 12,010 feet and John is now almost 300 feet higher at 12,308 ft.

There is still just over five minutes to go, so let’s jump to the last checkpoint before the finish.  We’re now 25 minutes into the glide:

John expanded his lead to 3 miles (5 km).  He’s been flying close to Vne and is now also dropping altitude more quickly.  John’s altitude is now 9,365 ft and I am now almost 1000 ft higher at 10,327 ft.

It’s now obvious that John is clearly ahead and I can’t do anything to catch up.  Let’s look at the finish line:

John is crossing the finish at 16:40:11 at an altitude of 9,221 ft. My position is shown at 16:37:11 (exactly 3 minutes earlier to maintain the same 3:00 minute difference that we have started out with).  I’m still exactly 3 miles (5 km) behind and at 9,983 ft.

I will cross the finish line at 16:38:30 at an altitude of 9,671 ft.

John’s 93km glide took him a total of 25 minutes and 30 seconds, and mine tool 26 minutes and 49 seconds.  In other words, the entire final glide took me 1 minute and 19 seconds longer than it took John.   The difference of 1 minute and 19 seconds is 5.1% (79 seconds / 1530 seconds).

5.1% is quite significant but it is clearly less than the published polar curves suggest, especially if John flew close to maximum wing loading.

In addition we can see that John also lost 532 ft more altitude than I did during the final glide (John lost 7287 ft whereas I lost 6755 ft).

It would be tempting to say that at John’s average climb rate of 490 fpm for the entire flight, it would have taken him 1 minute and 5 seconds to gain that 532 ft of altitude and the net advantage of his JS3 on final glide was therefore only 14 seconds (1:19 minus 1:05 minutes) – i.e. only 0.9% (14/1530 seconds).

However, such an argument – while mathematically correct – would miss the point that flying faster at a speed that would have resulted in an additional loss of 532 feet would not have allowed me to reduce my finishing time difference from 1:19 minutes to just 14 seconds.  The reason is that the speed polar drops off quite steeply at such high speeds.  A better way to save time would have been for me to just not do that one pointless exploratory turn.  This one turn cost me 50 seconds and netted no altitude gain at all.  Omitting this turn alone would have reduced my finishing gap from 1:19 to 29 seconds.

In summary I can say that my Ventus 2cxT held up quite well against John’s JS3.  In other words, it confirms that John’s superior performance over the entire flight has much more to do with pilot skill (e.g. during John’s only turn during the glide he gained 700 feet in 70 seconds compared to my 0 ft gain in 50 seconds) than with any performance advantage that his JS3 may have over my Ventus 2cxT.  This also is confirmed by my prior analysis of all other aspects of this flight.

Clearly, this analysis is just based on one flight and not under “laboratory” conditions.  It is not scientifically valid because not all variables were “held equal.” We did fly three minutes apart and it is possible (tough doubtful) that the conditions were more favorable three minutes earlier.  We also took a slightly different line above the Wasatch Plateau and I might have gotten lucky.  But I doubt it.  I’m fairly confident that the performance difference between the two gliders is exaggerated. If anyone wants to do the performance analysis for themselves, the flight traces can be found here:  John Seaborn’s trace and Clemens Ceipek’s trace.

On June 6 I published a “Beginner’s Guide to Scoring Well in the OLC Speed League“. This was – at least in part – written for myself as a guide for how to improve my own contribution.  Now that the Speed League is over it is a good time to take stock and ask “How Did I Do?” and “What Have I Learned?”

Boulder Achieved 2nd Place World-Wide, Out of 1029 Clubs

First of all, credit is due to my club, the Soaring Society of Boulder (SSB).  Out of 1029 participating soaring clubs competing in the World League, Boulder came in second place, beaten only by the outstanding team from the Minden Soaring Club.  Boulder has been doing well in the Speed League for many years but this is the best result for the Soaring Society of Boulder since OLC was created.

After a 9th place finish in Round 1, Boulder took the overall lead in Round 2 and then managed to hold on to first place until Round 9 when the soaring gods unfortunately had nothing but rain in store along the Colorado Front Range.  That gave Minden an opportunity to take the lead in Round 10, and Boulder was not able to catch back up.

The following table ranks the top 30 clubs in the 2020 World League.  The list includes 29 soaring clubs in Germany, seven in the western United States (Minden, Boulder, Tucson, Black Forest, Moriarty, Tehachapi, and Northern Utah), and one in Finland.

The full results can be found here.  Boulder came also second in the US Gold League, likewise only beaten by Minden.  The results are here.

How Did I Do?

One of my goals for the year was to make a significant contribution to SSB’s League Results.  I wanted to measure this specifically by scoring among the top three SSB pilots on 10 of the 19 planned Speed League Weekends in 2020. (The top scores of three different pilots affiliated with a specific club count for the club’s overall results – hence my objective to be among the three pilots whose results get counted.)

The Covid pandemic caused a six week delay in the start of the Speed League and the League was shortened from 19 weeks to only 13 weeks.  I therefore adjusted my goal accordingly to score among the top three Boulder pilots on seven of them.

I was able to fly on 10 of the 13 weekends.  And I did achieve my goal of seven scores among the top three participants:

I had two first place results (Round 3 and Round 7), four second place results (Rounds 1, 2, 6 and 8) and one third place result (Round 4).  In addition (not counted), I also came in second in the rained-out Round 9 when none of the Boulder pilots achieved a qualifying score (a minimum of 40 points).

Over the course of the season, 24 individual Boulder pilots contributed to SSB’s overall team score.  This is more than ever before and shows the breadth of SSB’s soaring talent.  The following table lists the top 10 contributors sorted by their “Contributing Points”, i.e. the cumulative number of OLC Speed Points for those rounds when the pilot’s score was among the top 3 SSB results.  By this metric, I was among the top three contributors of my club behind CX and BC.

Legend:

• • “Rounds Flown” indicates the number of rounds that a particular pilot participated in and achieved a Speed League Score of at least 40 points.  Only flights on Saturdays and Sundays during the 13 week long Speed-League Season count.
  • “Rounds Among Top 3” indicates on how many weekends a pilot’s score was among the best three results; i.e. their score ultimately “counted” for SSB’s overall Speed League Score for that particular weekend.
  • “Total Points Earned” is the cumulative number of Speed League Points a particular pilot earned for all their flights during the entire Speed League Season (remember, only flights on Saturdays and Sundays count).
  • “Contributing Points (In Top 3)” is the cumulative number of Speed League Points of a particular pilot for those weekends when their flight was among the top 3 SSB results. Note: if a pilot would score among the top 3 pilots on every one of the weekend that they flew, their number of Contributing Points would be equal to their number of Points Earned.  The fact that only one pilot scored among the top 3 on every weekend they flew (XR) underscores the breadth of overall team member participation.
  • “Contribution Per Round Flown” simply divides the “Contributing Points” of a pilot by the total number of rounds that they participated in.
  • “Contribution Per Round (Top 3)” divides the “Contributing Points” by the number of rounds when they scored among the top 3 SSB pilots, i.e. the number of rounds when their results counted.

Given that this has only been my third cross-country season I am definitely happy with my result.  However, the point of this analysis is not to congratulate myself but to determine how I can improve going forward.

What Did I Learn?

I took a close look at eight speed league weekends when there were enough comparable flights to assess my performance against that of other pilots. Why only 8 instead of the 10 that I participated in?  I removed the Speed League weekend when I flew from Nephi because my flight would not be comparable to those flying from Boulder.  And I removed one weekend when I broke off my flight after 90 minutes due to thunderstorms.  (Speed League Scoring is based on the best 2 1/2 hours, and my 90 minute flight would not have been comparable.)

To ensure a good dataset, my analysis only includes flights flown from Boulder and only flights flown on the same days that I was flying.   My objective was to do an “apples to apples” analysis of specific flights, not a comprehensive analysis of all SSB Speed League Flights!  (E.g., None of John Seaborn’s winning speed league scores are included because they were not flown from Boulder. Also excluded are flights by any pilot on days that I did not fly at all. )

The following table shows a summary of key stats from the best 2 1/2 hour flight segments that are automatically selected by OLC.

Before we dive into the data, it is important to note that only the results of CX and BX are truly comparable to my own (V1) because only CX and BC flew on almost all of the days that I was flying.   (Y flew on 5 of the 8 days that I flew; AO, kW, and XR only flew on 2 of the 8 days that I flew.  It any of them wanted to draw conclusions about their relative performance it would be better to only look at flights on the days that they flew instead, and not at the aggregate results across rounds that they did not participate in.)

With that caveat out of the way, what do the data actually tell?

First, they show that I (V1) had the lowest circling percentage of any pilot at only 13% and the Highest Effective Glide Ratio of 172:1.  This is indicative of a certain flying style that prioritizes staying in rising air and – probably – flying relatively slowly, and possibly also accepting significant course deviations.

I already noticed the same tendency in my race analysis of the Nephi Practice Day on July 1.  There, too, did I have the lowest circling percentage and the highest effective glide ratio in cruise flight.

Unfortunately, as I pointed out in the aforementioned article, circling percentage and effective glide ratio are both composite metrics that are not only based on a pilot’s ability to follow energy lines, but are also a function of a pilot’s inter-thermal cruise speed. To truly understand a pilot’s ability to follow energy lines we must look at the average “netto” value while in cruise flight because this metric is independent of a pilot’s chosen flying speed.

Unfortunately, the OLC flight analysis does not provide the netto value.

Second, the table above shows that my 5.7 kt average climb rate in thermals was fairly competitive as well.  Only CX climbed a bit better at 5.9 kt average, and kW had an outstanding average climb rate on one of his two flights resulting in an average of 6.5 kt.

Based on the flight stats that OLC provides it is impossible to tell why my average League Points per flight trailed the performances of CX, kW, and XR.

Multiple possible reasons come to mind:

• • Sub-optimal cruise speed between thermals (possibly too slow)
  • More course deviations than other pilots
  • Too much time lost in thermal tries
  • Other factors

Unfortunately, OLC does not provide any data to gain insights into these potential factors.

In search for more answers, I turned to See You’s flight analysis software from Naviter.  However, See You cannot isolate the best 2 1/2 hour OLC Speed League Segment and so it is necessary to examine the entire flight instead.  This may not be too bad except that pilots tend to disregard competitive considerations once they have exhausted their 4 speed league segments.  E.g., in Boulder it is not uncommon for pilots to loose many thousands of feet of altitude at the end of their flight by deliberately following lines of sink instead of lines of lift.  Or they simply pull out the spoilers to lose excess altitude.  Needless to say, such actions distort any performance analysis.  In addition, Boulder is notorious for difficult climbs at the beginning of a flight until the pilot is “connected” with the upper level lift band. Pilots who get “stuck” early in their flight often spend an hour or more in weak lift trying to climb out while others take a higher tow and find good lift straight away.  These factors also distort the analysis.  It would therefore be much better to isolate the speed league segments only and be able to analyze the flying performance just for the part of the flight that actually “counts”.

So everything from here on must be viewed with these caveats in mind.

Circling Performance

As we’ve seen above, I only circled 13% of the time during the Speed League segments of my flight.  The relative impact of my circling performance is therefore lower than it would be if thermaling had accounted for a larger proportion of my flights.

The following table compares my circling performance to that of the other pilots flying on the same eight days.

Interestingly, my average circling percentage only goes up from 13% to 16% if I look at the entirety of my flights.  This is somewhat surprising because it includes the initial climb-out phase, and suggests that I was on average lucky to find good thermals soon after releasing from tow.

Most of the other metrics also show favorable results for V1.

• • My average climb rate is shown as being the highest of all pilots.  I do not put all too much stock in this metric though because this metric can be easily distorted by several factors.  I already mentioned the initial climb out when it is fairly common to spend 30-60 minutes or even more in very weak lift (1 kt or even less) before getting into “good air” on the west side of the Front Range convergence. Another potential distortion can occur when a pilot deliberately circles to lose altitude prior to landing.  See You will treat this just like thermaling and the result is that the data unfortunately becomes useless for comparison purposes.
  • I calculated the “Average Loss Ratio” in thermals as the ratio of altitude lost compared to altitude gained while thermaling.  I think of this as a metric of effective thermal centering:  the lower the loss ratio, the better the thermals are centered because the glider is in lift most of the time while circling.  The data shows that only CX had an equally low loss ratio in thermals.  (However, the caveats mentioned above apply here as well.)
  • “Average Tries” measures how much time during the flight gets wasted by trying out (and ultimately rejecting) thermals.  See You uses 45 seconds as the “cut off” time; i.e. if the pilot circles for less than 45 seconds before moving ahead on course this is deemed to be a “try”.    At 2.5% my “Average Tries” percentage might be a bit higher than I think it should be.  CX spent only half as much time trying out thermals.  However, I’m not sure what value is ideal.  At first glance it would seem that the lower the better, but a very low tries percentage could also suggest that a pilot is not rejecting enough weak thermals.  (This would show up as a low average climb rate, which is certainly not the case for CX.)
  • “Average Altitude Gained/Lost During Tries” subtracts altitude losses from altitude gains during tries and calculates an average value per flight. I was a little surprised to see that the value was overall positive for my tries which suggests that I rejected weak climbs but that I did not lose altitude during these tries in aggregate.  Most other pilots did lose more altitude than they gained during their tries.

Overall, I’m not sure that the Circling Performance Analysis provides strong indicators that would suggest specific improvement opportunities.  Cutting my “tries” percentage may help but only if it doesn’t lead me to reject really good thermals as well.

I believe there exist are other improvement opportunities for me but they are not specifically suggested by the data.  E.g., I believe I could achieve better climb rates by tightening my circles, and flying slower in thermals.  But to see this I would need to be able to compare my orbit times and ground speed in thermals to that of other pilots, especially in correlation to effective climb rates achieved.  I also believe that I can further improve my aileron/rudder coordination in thermaling flight.

Cruise Performance

If the thermaling analysis is somewhat inconclusive in terms of identifying improvement opportunities, maybe more can be gleaned from an analysis of the cruise flight segments.  Let’s look at the table below.

The first thing that jumped out to me is that my Average Effective Glide Ratio is still by far the best of any pilot (not surprising given that I also had the lowest circling percentage – which really is just the mirror image of this metric), but that my netto value is not as high as that of CX and XR.

As I mentioned before, netto is a much better metric to look at than effective glide ratio or thermaling percentage because it much better isolates a pilot’s ability to follow energy line.

A difference of 0.1 kt is certainly not a huge negative but it adds up, especially if one spends most of the time cruising!  Consider this: since my thermaling percentage is only 16%, I spend 84% of my flight time in cruise flight.  In other words: in aggregate, I cruise more than 5x longer than I circle (84/16=5.2).  So, when the cruise percentage is that high, over the duration of an entire flight a 0.1 kt vertical speed difference while cruising is approx. equivalent to a 0.5 kt vertical speed difference while climbing!  Looked at this way, it’s definitely not irrelevant.

On the other hand, the data set is not large enough to draw any conclusions.  Following energy lines is as much an art as it is a science and the location and strength of energy lines is so variable that an analysis of just eight OLC flights (where each pilot flies at different locations and at different times within a very wide area) is certainly limited with respect to assessing skills of improvement opportunities.

What we can say from the data, however, is that the effective glide ratio is likely very significantly impacted by the average cruise speed:  CX had the best netto value (1.6 vs 1.5 for V1) but his average effective glide ratio was significantly worse than mine (63 vs 107).  The main difference is most likely CX’s higher average cruise speed (83 kts vs 79 kts after adjusting for the glider’s index). The higher cruise speed resulted in a higher sink rate during cruise, therefore a lower effective glide ratio, and hence more time spent circling. Still, CX had the overall better performance so it is likely that his combination of flying speed and climb rate in thermals gave him an overall edge.

Another possible explanation for the difference in performance is the percentage of course deviations.  This seems such an obvious potential differentiator that one would think that the flight analysis software would provide this metric! Unfortunately this is not the case and there is no practical way to compare the extent of course deviations over eight flights manually.

Conclusion

Unfortunately, the insights gained from a detailed analysis of eight Speed League Flights are inconclusive with respect to truly understanding the performance differences and identifying specific areas for improvement.

The data suggest that my strengths include the ability to follow energy lines and centering thermals.  This is also consistent with my findings in Nephi. These are core skills that have a very significant impact on overall performance and are key pillars of my current performance.

In addition to further honing these strengths, I believe I can further improve in the following areas.  However, better flight analysis tools would be needed to confirm that these are more than “hunches”:

Thermaling:

• • Better use of the full height band (increase in average climb height per thermal) / more selective in accepting thermals
  • Tighter circling (shorter orbit times – aim for around 25-27 seconds when ballasted, less without ballast.)
  • Slower orbiting speed (e.g. stall speed for the applicable bank angle and wing loading plus ~2 kts)
  • Further improvement in aileron/rudder coordination

Tries:

• • Slightly reduce number of tries (but don’t aim for zero!)

Cruise:

• • Increased cruise speed, even when flying in lift along energy lines, with more aggressive pull ups in strong lift
  • Possibly reduce course deviations (need to be able to measure)

Appendix

Opportunities for Providers of Flight Analysis Software – Especially for OLC!

To perform a more insightful analysis of OLC flights, a software would have to be able to isolate the portion of the flight that is scored by OLC.  I.e., for Speed League Scores it would be necessary to specifically analyze the performance during the 2 1/2 hour Speed League segment (maximum of four legs as defined by OLC rules).  For OLC plus flights, the relevant six legs would need to be isolated, again, based on the same rules that OLC applies.   Once that is accomplished, the software would have to be able to calculate the following key data points:

Thermalling:

• • Average climb rate in thermals;  (ideally also the median climb rate)
  • Circling Percentage
  • % time spent in weak / medium / strong thermals (e.g. <2.5 kts; 2.5-5 kts; >5 kts). This is of interest because time spent in weak thermals is the #1 speed killer.
  • Average orbit time in thermals – a measure of how close one is able to fly to the core
  • Average speed while circling in thermals (air speed or ground speed) – in conjunction with orbit time another key metric to measure one’s ability to stay close to the core
  • Number of thermals
  • Average height gain per thermal – this is important to understand how much of the lift band one is able to exploit; greater height gain means fewer thermals, which fewer centering losses
  • Loss ratio (altitude lost / altitude gained while thermaling) – a measure for one’s ability to center thermals and keep them centered

Isolate Tries from Thermals and from Cruise:

• • % time in tries
  • Number of tries
  • Altitude gain – altitude loss in tries

Cruise:

• • % time in cruise flight
  • Netto during cruise flight only (excluding thermals and in thermal tries)
  • % course deviation (i.e. actual course track flown / scoring distance)
  • % time in netto rising air, and ideally also:
    • % time in weak / medium / strong lift (e.g. <2.5 kts; 2.5-5 kts; >5 kts)
    • % time in weak / medium / strong sink (e.g. <2.5 kts; 2.5-5 kts; >5 kts)
  • Average cruise distance between thermals (excluding tries)
  • Effective glide ratio (but this has mostly entertainment value)

OLC already has an enormous repository of flight data and would be in an excellent position to provide these analysis tools.  Introducing such tools as a subscription offering could also be a revenue opportunity for OLC.  Such a tool could allow pilots to benchmark their flights against those of others who flew in the same area on the same day.  I believe this would be a highly valuable add on and many pilots would be willing to pay extra for such insights.

Introducing such a tool could also pave the way for additional “big data” analyses of OLC flight traces.  The opportunities to provide deep insights are enormous. E.g., flight traces could be used to create “heat maps” of “house thermals” or other highly active thermal areas.  Frequently flown XC routes could be identified similar to how Strava shows routes that are frequented by runners or bicyclists.  Anyone who’s exploring a new area, taking a soaring vacation, or just simply planning cross country flights would find huge value in such tools.

It would be easy to anonymize the data that is being used for such analyses such that data privacy considerations can be addressed.

Unfortunately OLC is not (yet) taking advantage of its data repository. Worse, by limiting flight trace downloads to 20 per day it even prevents soaring pilots from exploiting this treasure trove of data on their own.  There’s a tremendous opportunity to create real value for the soaring community. I hope someone will!

Covid destroyed my plans to fly my first two soaring contests in 2020 – the 20m-2-Seater-Nationals in Montague, CA as well as the Region 9 Sports Class Contest in Nephi, UT.  Both of these contests were postponed to 2021.

But there was one day in 2020 when I did fly in a friendly race: a bunch of pilots including myself made their way to Nephi for a practice week in preparation for next year’s contests.  And on July 1 the organizers declared a contest task fit for the 18 meter class.  It was the only day of the year where I flew exactly the same task as several other pilots.  One day isn’t much to go by, but I wouldn’t be me if I skipped the opportunity to analyze the results.  Especially since one of the pilots was John Seaborn, a multiple National Champion, and a fellow Boulder pilot. Don’t pass up an opportunity to learn!

The Task

The task was a Turn Area Task (TAT, aka AAT) with three assigned turn areas:

• • Start: 04 SE Start – radius 5 miles
  • TP1: 66 Nine Mile Ranch – radius 20 miles
  • TP2: 81 Table Mountain – radius 20 miles
  • TP3: 15 Browns Peak – radius 5 miles
  • Finish: 05 Finish (i.e. Nephi Airport) – radius 2 miles

Task Distance: from 275.2 miles minimum to 447 miles maximum (364.4 miles from the center of each turn area to the next)

Minimum Task Time: 3 hours (this seemed extremely short to me based on the task distance, so I basically decided to ignore it and just fly around the task as fast as possible). There was no declared maximum start altitude.

The Pilots

There were 18 pilots flying from Nephi that day.  However, flying the task was entirely voluntary and I don’t know how many attempted it.

At least six pilots uploaded flight tracks to OLC that show valid task declarations for this particular task in their flight recorders. Five of them finished the task.  I based my analysis on the five finishers because these flights are most directly comparable.

• Pilot A, Hph 304 SJ 18 meter.  Current Pilot Ranking: 91. Holds FAI 1000km Diploma. Several top 5 finishes at Sports Class contests
• Pilot B, LS3a 15 meter. No information found on the SSA website.
• Pilot C, Ventus 2cxa FES 18 meter. Current Pilot Ranking: 73. Participated at several Regional Contests.
• Pilot D, JS3 18 meter. Current Pilot Ranking: 100.  Multiple National Champion. World Championship Contender.
• Pilot E, Ventus 2cxT 18 meter. No Pilot Ranking.

I am pilot E. 😉

Overall Results

I have attempted to score the flight according to SSA Sports Class rules and applied handicaps for the gliders (because one of them was an older 15m ship that clearly was not competitive with the 18 m gliders of the other 4 contenders.

These were the results (provided that I did the scoring correctly which is, frankly, insanely complicated):

1. 1st Place: Pilot D.  1000 points (blue trace)
2. 2nd Place: Pilot E. 823 points (purple trace)
3. 3rd Place: Pilot A. 804 points (red trace)
4. 4th Place: Pilot C. 783 points (green trace)
5. 5th Place: Pilot B. 614 points (yellow trace)

The following table shows the raw speeds (before applying the handicap) and is easier to understand:

Not surprisingly, Pilot D – the multiple National Champion, let’s correctly identify him as John Seaborn :-), posted the fastest speed, and won by a wide margin.

Pilots A, C, and E were fairly close together (separated by 3.5 kts or 40 points), but far behind John. I was quite pleasantly surprised to find that I came in 2nd place, even though my performance was vastly inferior to John’s.

Pilot B was considerably behind everyone else.  However, his raw speed is not comparable because he flew an inferior glider (the 15m LS3a).

Analysis

Just looking at raw speeds and point totals doesn’t really teach me anything except that I can’t compete with John Seaborn.  But that I already knew.

So let’s dig a layer deeper and look at some key stats to see some of the differences, in order to understand why John was able to score so much better than anyone else.

(1) Cruise Speeds

Given that John’s average speed of 86 kts was more than 15 kts faster than that of any other pilot it would seem likely that he flew much faster between thermals.

And in fact, John did indeed fly much faster than anyone else:

John’s average indicated air speed in cruise flight was 92 kts, 16 kts faster than mine.

John was also 15.2 kts faster overall on average so at first glance it would be tempting to attribute John’s superior overall performance primarily to his higher cruising speed.

But beware! This line of thinking would be a big mistake!

Let’s figure out how my overall average speed would have been affected if I had matched John’s speed and flown 16 kts faster during my cruise segments.  Had I flown at 92 knots instead of 76 knots, my sink rate would have been about 110 fpm greater than it actually was.  (Based on the wing loading of my Ventus 2xcT with partial water ballast my sink rate at 76 kts IAS was about 180 fpm; at 92 kts IAS (John’s cruise speed) it would have been ~290 fpm).

While flying faster would have meant that my cruise time would have shrunk by 17.4% from 196 minutes to 162 minutes (i.e, by 34 minutes), I would have lost an additional 11,700 feet of altitude (162 min x 290 fpm – 196 min x 180 fpm).  At my average climb rate of 4.2 kts (~420 fpm), it would have taken me 28 minutes to regain that altitude.

This means, my overall flight duration would have improved only by about 6 minutes, not by 34 minutes!  My average speed would have increased from 70.8 knots to 72.7 knots.  A little faster, yes, but still nowhere near John’s performance.  My point total would have increased from 823 to 845.

In other words, John’s higher average cruising speed explains about 1.9 kts of the 15.2 kts speed difference between his flight and mine.  That is 12.5% of the  total performance difference.

BTW – this improvement assumes that I would have been able to maintain the same 4.2 kt climb average and not been tempted (or forced) to take weaker climbs as a result of losing altitude faster.

Let’s also calculate what would have happened had I flown just 5 kts faster:  81 kts instead of 76 kts IAS.  My cruise flight duration would have been 186 minutes (10 minutes shorter) but my sink rate would have been approx. 25 fpm worse (based on my glider’s speed polar at my actual wing loading). In this case I would have lost an additional 2,850 ft over the course of the flight (196×180-186×205=2850), which would have taken me close to 7 minutes to regain while circling (2850/420=6.8). I.e., I would have saved a little over 3 minutes in total.

So, could or should I have flown faster.  Yes.  Would it have had a big impact? Probably not. Would it have made me as fast as John? Most definitely not!

The reality is that modest variations in average cruise speed by 5%, 10% or even 15% have only a fairly minor impact on the overall average performance because they are largely offset by the glider’s varying sink rates at different air speeds.  McCready’s speed to fly theory is of course accurate but its importance tends to be overrated. Especially because there is also a strategic price to pay for faster cruise speeds:  because the glider sinks faster to the ground the pilot has fewer options to select suitable thermals. This means that the faster flying pilot may find high average climb rates more difficult to attain. He or she also faces a higher land-out risk.

So, if John’s higher cruise speed wasn’t the main reason for his superior performance (it wasn’t), then what was?  Let’s look at other potential reasons below.

(2) Flight Duration

In a Turn Area Task with a minimum task time, flight duration is a relevant factor.  The minimum task duration was 3 hours, and John optimized his time quite well – although he would have scored even higher had he flown the full 3 hours and not finished 1 minute and 10 seconds too early.  In fact, had he flown exactly three hours his average speed would have been 86.6 kts instead of 86.0 kts (assuming that he had enough altitude to extend his flight just a little at the last turn point – as in fact, he did).  0.6 kts may not sound much but it could make a crucial difference if the results are very close. (Per my calculations, the point difference between John and the other pilots would have been 6 points greater had he finished at an average speed of 86.6 kts instead of 86.0 kts).

Coming in “right on time” (or slightly above) is usually an advantage because the start altitude is considerably higher than the finish altitude and a pilot who flies just the minimum time (and no longer) is best able to convert that altitude difference into a higher average speed.

How big is this effect on a 3 hour task?  Not insignificant.  Math guru John Cochrane has done the work and given us some formulas to estimate the effect.  On a three hour task in western conditions, the cost tends to be about 0.5 score points per minute of overtime.  I.e. my 50 minutes of overtime might have cost me about 25 points.  I.e., instead of being 177 points behind John, I might have only been 152 points behind, had I been able to finish the task in 3 hours instead of taking 3 hours and 50 minutes.

In other words: my 50 minutes of overtime explains about 14% of the overall performance difference between myself and John.

(2) Circling Percentage

A popular metric to compare flights of different gliders is to look at the amount of time pilots spend circling versus cruising.  Since you’re not moving forward while you go around in circles, a high circling percentage tends to be a disadvantage.

John’s circling percentage was indeed quite low: 20%. However, it was not the lowest. In fact, I spent even less relative time circling than John did: only 15%!

But did this lower circling percentage give me a demonstrable advantage?  Unfortunately that is impossible to say!  The problem with the metric “circling percentage” is that it is a complex data point – a composite of several factors that include not only route selection (e.g. flying through lift vs sink), but also flying speed (if you fly slower your sink rate is lower, i.e., you arrive at the next thermal higher, and you need to circle less.)

Because of its composite nature it is impossible to say that the pilot with the lower circling percentage necessarily gains an overall advantage.

(3) Effective Glide Ratio

Highly related to the circling percentage is the effective glide ratio achieved in cruising flight.  This is in part a measure of how effectively a pilot is able to follow energy lines, but, just like the circling percentage, it is also a composite metric driven in part by the inter-thermal cruise speed.

The more effective one is at following energy lines, but also, the slower one flies, the less one needs to circle and the higher the effective glide ratio.  And indeed, the results show a mirror image of the circling percentage:

My effective glide ratio of 93:1 was better than anyone else’s.  John’s 79:1 came second.  However, just like the circling percentage, this metric ultimately doesn’t mean very much.

(Note: a reader might wonder how it is possible to achieve such high effective glide ratios with gliders that have a “best” glide ratio of around 50:1 when flown at best L/D speed (i.e. much slower than we were flying). The answer, of course, has to do with the pilot’s ability to follow energy lines – areas where the air is on average rising instead of sinking or just standing still.  More about that right below.)

(4) Following Energy Lines

The circling percentage and the effective glide ratio might be taken to mean that I did better than anyone else in terms of following the best energy lines.  However, as I mentioned, both metrics combine the effects of following energy lines and the actual inter-thermal cruise speed.

A much purer measure for the ability to follow energy lines is the netto value during the straight flight segments.  Netto measures the actual vertical movement of the air that the glider flies through and is not impacted by the glider’s sink rate.  Hence, it just measures the effectiveness of the choice of route and is thus a much better metric to use.

This table shows that it was John who did the best job with respect to following energy lines.  During all of John’s straight flying segments the air rose at an average rate of 2.1 kts.  On this measure Pilot A ranked second with an average netto value of 1.8.  Pilots C and E (myself) were tied in third place with a netto value of 1.6 kts.

How much difference did this make?  John spent 2 hours and 22 minutes in straight flight.  During that time the airmass he flew through went up by an average value of 2.1 kts, approx. 210 fpm.  That is 50 fpm more than during my flight where it went up on average by 160 fpm.  Over John’s entire task this difference amounts to 7,100 feet (50 fpm x 142 minutes).  At my average climb rate of 4.2 kts (~420 fpm)  – see below – I needed 17 minutes to climb 7,100 feet.  On a 3 hour task, 17 minutes equals 9.4% (17/180).   And 9.4% is the difference between John’s winning speed of 86 kts and a speed of 78 kts.

In other words, John’s superior performance with respect to following energy lines explains 8 kts (more than 50%) of the 15.2 kts speed difference between our two flights.  It is thus the single most significant factor of John’s overall superior performance!

Since this is such a hugely important factor I also tried to understand specifically what John did better in terms of following energy lines.  This is very difficult to glean from the data alone but I was able to combine evidence from the flight trace and an analysis of my inflight video recording. Let’s take a closer look.

The following graph overlays the flight traces of John and I.  John’s trace is shown in red and my trace is shown in blue.

The graph above indicates where John and I made different route choices, especially with respect to approaching the first turn area (top right) and the second turn area (bottom left).  But it tells us nothing as to which of the two traces followed better energy lines.

Fortunately, SeeYou (the flight analysis software from Naviter) allows us to display the traces based on their netto values as well.  This is shown in the graph below.

You have to be careful to remember which trace belongs to which pilot. That’s why I included the graph earlier that clearly shows which of the two traces belongs to John and which one belongs to myself.

At first glance there doesn’t appear to be too much difference.  But if we take a closer look at the approaches to TP1 and TP2, we can see some subtle differences in the color gradient.

Let’s look at the approach to TP1 first:

The differences are subtle but it you look carefully, you can see that my trace (the one further north) towards and away from TP 1 contains somewhat more blue segments than John’s (the one further south).

(Note: you can also see that I wasted quite a bit of time after turning TP1 trying to climb.  I was uncomfortable with my altitude and made a number of unsuccessful exploratory turns.  This was another contributing factor to my overall performance; it is discussed below under point (5) Climbing).

One might wonder: why did I fly such a northerly line to TP1, just barely nicking it and then heading back west?  The answer is in the following image, taken a few minutes before I turned right to nick the the turn area:

To get to TP1 I followed a cloud street to the northeast, which ran past the turn area to its north.  The turn area itself was in the blue to the right in the picture above.

Why did John decide not to follow the same line?  I don’t know for sure but I can speculate.  Let’s come back to this below after discussing TP2.

Here’s our different approaches to TP2.  Let’s look at the graph:

John’s trace is the one further east (right), and mine is the one further west (left). Once again you can see that there seems to be a bit more blue in my trace than in John’s trace.

Why did John take the easterly route while I took a more westerly line? Here’s what the sky ahead looked like as I was heading towards TP2:

In the picture above I am about 25 miles north of TP2.  I dare say there wasn’t much to go by to determine what route to take.  The sky was entirely blue.  I simply stayed above the high ground of the Wasatch Plateau and took pretty much every lift I could find to stay high.

As you can see from the trace, John flew a more easterly line.  Did he know something that I didn’t?

Here is the answer: John had started the task much later than I did and came to the same area about 20 minutes after I did.  Here is what the sky looked like by the time John was still about 25 miles further north:

A nice line of clouds developed further east that had not existed earlier.  John could see the clouds ahead and was able to follow them while I was already too close to the turn area by the time the clouds appeared.

This means that a key reason why John was able to find a better line to and from TP 2 was that he timed the start of his task better:  while I made the rookie mistake of starting as soon as I was up and seeing a path to get to TP1, John decided to wait for the day to develop further.  As it turned out, these 20 minutes played a big role!

Let’s revisit the approach to TP1 as well: I believe, John’s later start also allowed him to fly a more direct route into the first turn area.

The above image shows John’s trace.  Note the 90 degree kink in the line near Brown’s Peak on the left.  This is just speculation but I think that John may have changed his course because he could see the first cloud appear in the turn area, which had been completely blue when I approached it earlier.  You can see that John also didn’t just “nick” the turn area but continued into it for a few miles where he climbed in good lift.  I have to believe that a cumulus had formed by the time he entered the turn area (almost one hour later in the day than I did).  This would underscore the advantage one can gain by starting later and letting the day develop before going on task.  (Obviously this makes only sense when the better part of the day is ahead and there is no risk of being unable to finish.)

Note that by flying a direct line to TP1, John was also able to reduce the total task distance and finish much closer to the minimum finishing time.  Had he continued to the northern edge of the turn area (as I did), John would also have finished with overtime.  I discussed the advantage of finishing on time in Section (2) above.

In summary I conclude that John’s decision to start the task later was a key factor helping him follow better energy lines, because he was able to follow cloud lines that had not existed earlier and thereby increase the ratio of flying in lift vs. in sink.

(5) Climbing

Pilots who are able to thermal better than their competitors can also gain a major advantage.  And indeed, John’s average climb rate of 4.9 was clearly better than anyone else’s:

The delta between John’s climb rate and mine is 0.7 kts or 70 ft per minute, just over 1 ft per second.  This may not sound like much but it adds up.  John spent 36.6 minutes circling.  In that time he gained about 2,500 ft more than I did (36.6×70=2562).  Which means: I would have needed six minutes longer to achieve the same gain of height (2562/420=6.1).   On a 3 hour task, six minutes are 3.3% or the difference between 86 kts (John’s winning speed) and 83.2 kts.

In other words, John’s superior climb performance explains 2.8 kts (almost 20%) of the 15.2 kts speed difference between our two flights.

Once again, I tried to dig a little deeper.  Did John actually center the thermals better or did he just do a better job at thermal selection?

The data point to both being factors:  John spent most of his circling time in 5, 6, and 7 kt thermals; whereas I spent most circling time in 4, 5, and 6 kt thermals.  I also wasted about 10 minutes trying to climb in sinking air and lost a total of 1500 ft whereas John wasted only 5 minutes this way and only lost 200 feet.

I lost this wasted time in two places: (1) when I got lower than I liked coming out of TP1 with still some blue sky to cross ahead, and (2) when I tried to stay high prior to TP 2 with only blue sky ahead.  (A later start may have helped reduce some of the wasted time because clearly marked thermals ahead would have given me more confidence and lessened the impetus to try every lift that I encountered in the blue.)

This difference of 1300 feet extra wasted explains approx. another 10% (or 1.5 kts) of the delta between John’s performance and mine.  The additional 5 minutes wasted account for another 3% (or 0.4 knots).

John also took only 14 thermals with an average altitude gain of 1300 feet per thermal and flew on average 23 miles between thermals whereas I took 19 thermals with an average altitude gain of less than 800 feet per thermal and only flew 18 miles between thermals.  This is illustrative of my overly conservative flying style.  (Another indicator is that my thermal entry altitude was consistently about 1000 feet higher than John’s.)

The number of thermals chosen and the average altitude gained per thermal do not impact the overall performance “per se”.  But they are an important reason as to why my average climb rate was lower than John’s:  each time you stop to thermal you have to first center the thermal before you can get the most out of it.  John did this 14 times and I did it 19 times.  It goes to reason that centering more thermals made my climbs less efficient and is a significant contributor to John’s superior climb rate.

(6) Other Potential Factors

(a) Speed Variations in Cruise Flight

One might think that pilots could gain a significant advantage by really slowing down in rising air and speeding up in sinking air.  However, the following chart shows that none of the five pilots varied the speed significantly from their average cruise speeds while flying through rising and sinking air.  The data are in kts IAS relative to the average IAS flown by each pilot.

I was especially surprised to see that none of the pilots sped up much while flying through sink.

I think the problem is that varying the cruise speed between lift and sink works great in theory but  is very difficult to do in practice.  If you find yourself in sink and speed up, chances are that you fly too fast through the next patch of rising air. Conversely, if you’re flying in lift and slow down, it’s quite possible that the lift will have ended by the time your speed has come down and now you’re going too slow in sink.  In the soaring literature this is often referred to as “chasing MC speed” and I am not the first one to observe that it doesn’t really work in real life.  In addition to always lagging behind in your reaction it is also inefficient to constantly vary your speed by pushing and pulling.  Obviously, it does make sense to vary your speed if you positively know what’s just ahead (e.g. if you’re closely following another glider and can observe it rising or falling). But in the absence of compelling clues it is often better to just maintain your speed during cruise.

(b) Tactical Turn Point Height

Turn Point 2 was located directly into a 13-16 kt headwind from SSW and provided an opportunity to gain an advantage by rounding the turn point low and then using the tailwind to gain altitude while moving on towards Turn Point 3.

The table above shows relatively small altitude differences among the various pilots when rounding TP2 and suggests that none of the pilots gained a tactical advantage.   Turn Points 1 and 3 offered much less opportunity to gain an advantage.

(c) Start Timing

John Seaborn was the only one of the five pilots who seemed to deliberately time the start based on improving soaring conditions.  Everyone else started right after gaining sufficient altitude to get going.

It is impossible to directly measure the impact of the different start times.  However, as we have seen, waiting to start late was likely a key underlying contributor to John’s superior performance as it helped him follow appropriate energy lines and improve his climb performance.

(d) Start and Finish Altitude

Since this was just a practice task, there was not a declared maximum start altitude although I suspect John deliberately started lower for practice reasons. A higher start altitude would have provided an advantage.

Minimum Finish Altitude was 7000 ft and most everyone returned significantly higher than that.  I remember there being a lot of lift on the final leg and I flew close to Vne or the altitude and I still came in more than 2,500 ft too high.  John was just a few miles behind me and flew through the same air, also finishing high.

By starting ~3000 ft higher than John and finishing ~500 ft higher I gained a net advantage of 2500 ft, which translates to a six minute time advantage in my favor (2500/420=5.9) and can alternatively also be expressed as a speed advantage of 2.8 kts in my favor.

Summary

George Moffat explained in his classic book “Winning II” (p. 42-50) that winning can be viewed as the result of not losing.  He illustrates that the winner of any particular flight usually did several or many things (big and small) a little better than his or her competitors, and that the win can therefore be explained as a sum of all these things.

If I contrast John’s flight with mine, here is a summary of the things that John did better than I, and how much each factor contributed to the overall results:

• • Following energy lines (measured by netto in cruise flight) … 8 kts
  • John climbed better (measured by average climb rate) … 2.8 kts
  • Time and altitude wasted in “trying out thermals” … 1.9 kts
  • Finishing on time vs. finishing with 50 min overtime … 1.7 kts
  • More optimal cruise speed … 1.9 kts

Total difference: 16.3 kts

As discussed I believe that John’s decision to delay the start of his task until 13:41 (53 minutes later than my start) contributed to his ability to follow better energy lines, finish closer to minimum time, reduce time wasted in exploring thermals in the blue, and possibly even achieve a higher average climb rate.

From the 16.3 kts we have to subtract factors where John put himself at a disadvantage:

• • Net difference in start/finish altitude … 2.8 kts
  • John finished 1 min 20 seconds under minimum time … 0.6 kts

In sum, the analysis explains 12.9 kts (16.3 – (2.8+0.6)) of the overall speed difference between our two flights while the actual speed difference was 15.2 kts.  This leaves just 2.3 kts of speed differential unexplained.

I believe that some of the unexplained 2.3 kts may be attributable to John’s slightly superior glider (a new JS3 vs compared to my 17-year old Ventus 2cxT) and potential differences in wing loading (I flew with 2/3 water ballast; I don’t know John’s wing loading but it may have been higher than mine).

Key Lessons

(1) Focus Most on What Matters Most: Energy Lines and Climb Rates!

This deep-dive analysis of one single flight suggests that the following two  factors have the biggest impact on overall performance:

• • The ability to follow energy lines (as measured by “netto” in cruise flight)
  • The ability to avoid weak climbs, minimize tries in sink, and achieve a high average climb rate (selecting the most appropriate start time can play a major contributing role)

These two things not only have the biggest impact, they are also skills that one must develop and hone over time. And they are relevant on every single flight.

Over the past two seasons I have significantly improved my ability to follow energy lines but I still have a ways to go as this one flight clearly shows.  Starting a task later in the day can make energy lines more visible.

I have also been working on improving my climb rate in thermals and there are still some low hanging fruit such as thermaling slower and tighter.  The data suggest that I also have an opportunity to become more selective: I should skip more of the weaker thermals and use more of the available altitude band.  It is best to only take thermals that offer an average or better climb rate.  And it is critical to minimize the time it takes to center them.  That’s why it is generally better to take fewer thermals. In contests it is often best to take thermals marked by other gliders, precisely because others have already done the centering work for you (obviously assuming that they did it right.)  I was actually encouraged to see that my avg climb rate was “only” 15% lower than John’s.

(2) Picking the “Right” Start Time

It seems that picking the right start time was a key underlying contributor that may have helped John achieve a superior performance – especially with respect to following energy lines and achieving a superior average climb performance.

(3) Other Tactical Improvement Opportunities

Compared to the overarching factors above, everything else is secondary (although, of course, it also adds up).  Interestingly, most of the other contributing factors are more tactical in nature and can be more readily improved by an average pilot, including:

• • Not leaving potential energy on the table by departing too low or finishing too high.  The departure altitude is relatively straightforward as in contests it tends to be a given. The finish is trickier and my conservative approach means that I am likely to come in too high.  I will need to practice more final glides to gain the confidence to finish close to the minimum finish altitude.
  • Optimizing the finish time (avoid under time; minimize over time).  I have been practicing a few TATs and they are more fun than I initially thought. On this particular flight I believe that a later start time might have helped me pick a shorter flight path and finish closer to minimum time.
  • Flying closer to MC speed.  The stats on this flight showed – once again – that I am among the more conservative XC pilots. There’s definitely some room for me to fly faster and take higher sporting risks.  However, the rewards of flying faster are not huge and I will always have to balance this against the added land-out risk and the risk of having to take weak climbs that could destroy my overall result.
  • Turning upwind turn points low and downwind turn points high. This did not play a big factor on this particular task, likely because TP2 (where it would have helped) was in the blue and I therefore tried to stay high.  However, from my experience with Condor I know that this tactic can have a significant impact on the overall result.
  • Speeding up in sink and slowing down in lift.  This is great in theory but the data suggest that it may be impractical to do this efficiently in reality, especially with a ballasted high performance glider. Lift and sink tend to alternate so quickly that it is often impossible to vary the airspeed in a timely manner.  There is nothing worse than pulling up in lift only to find oneself in sink again right when the glider has slowed down; or conversely, to push down in sink only to find oneself shooting through the next patch of lift at high speed.

(4) Don’t Look Too Much At Composite Metrics such as Glide Ratio and Circling Percentage

Composite metrics that I have liked to look at in the past such as circling percentage and effective glide ratio achieved, have more entertainment value than analytical value.  You won’t win a race because you have achieved the lowest circling percentage or the highest effective glide ratio.  You primarily win the race because you consistently flew through better air than your competitors (as measured by netto), and because you achieved a high average climb rate, especially by picking  a limited number of good thermals and successfully avoiding weak climbs.