(Editorial Note: since initial publication, I have added a few thoughts suggested by readers. Andy Blackburn’s input has been particularly valuable. I also added a post scriptum at the end with additional tips. Thank you to all who commented.)
Who has not heard of the MacCready Speed-To-Fly Theory? It is the brilliant discovery of a brilliant man who was not only the first American to become a world soaring champion but who came up with a scientific way to demonstrate how fast we should be flying in-between thermals in order to maximize our cross-country speed.

Not long after MacCready published his theory, other pilots followed his example and began equipping their gliders with “MacCready Rings”. These are simple devices mounted around a glider’s variometer telling the pilot how fast they should be flying depending on the expected strength of the next lift.
With the onset of flight computers, MacCready’s Speed-To-Fly Theory (or STF for short) went digital. Today, every flight computer requires the pilot to input their “MC value”, and every STF vario will produce audio and visual signals. These tell the pilot whether to speed up, slow down, or maintain the current speed – based on the MC value they selected.
Over time the application of STF theory has evolved a bit. E.g., pilots have learned that it is useful to slow down as they get closer to the ground to minimize the risk of a landout. Others correctly pointed out that “chasing the needle” is not only distracting but that constant control inputs make it inefficient as well. Instead, most would recommend flying at “block speeds” that approximately correspond to the correct MC setting. After all, flying a bit too slow or a bit too fast makes little difference in terms of the average speed achieved. Some have even come up with scientific ways to show when, how, and how much to deviate from MacCready’s theory. (E.g., see Daniel Sazhin’s and John Bird’s work about “Bounded Rationality and Risk Strategy in Thermal Soaring” or John Cochrane’s article, “MacCready Theory with Uncertain Lift and Limited Altitude“). Instead of getting into more details here, I recommend that interested readers take a look at the article “Just a Little Faster, Please“, also by John Cochrane.
However, no-one doubts that MacCready theory at its core is mathematically correct and scientifically sound. It remains the undisputed foundation of any theory about how fast we should fly in cruise. Most importantly: every flight computer and every vario asks you to input an MC value. So you better know what these devices are doing with the information you enter.
MacCready Theory in a Nutshell
Every soaring textbook has an explanation for how and why the theory works. In essence, it is quite simple: when the lift ahead promises to be strong you should fly faster. When the lift ahead looks to be weaker, you should fly closer to your glider’s best L/D speed, i.e. the speed where it has its best glide ratio. MC theory tells you exactly how fast you should fly based on the strength of lift you expect ahead.
The series of charts below illustrate a simple example. They are based on the speed polar of a Discus CS (one of the most popular standard class gliders) without water ballast. (The principles explained are the same for whatever glider you fly but the values will obviously differ. If you fly a similar glider, such as an LS4, a DG 300, or an ASW 24 they will be close. A DG 505’s polar is also similar.) The speed polar is the curved line in blue. It illustrates the rate of sink at various speeds. The speeds are on the horizontal axis (in kts), and the glider’s rate of sink at these speeds is shown on the vertical axis (also in kts). Using the same units on both axes (in this case kts) is very helpful because you can calculate the glide ratio at any point along the curve simply by contrasting the speed to the sink rate.
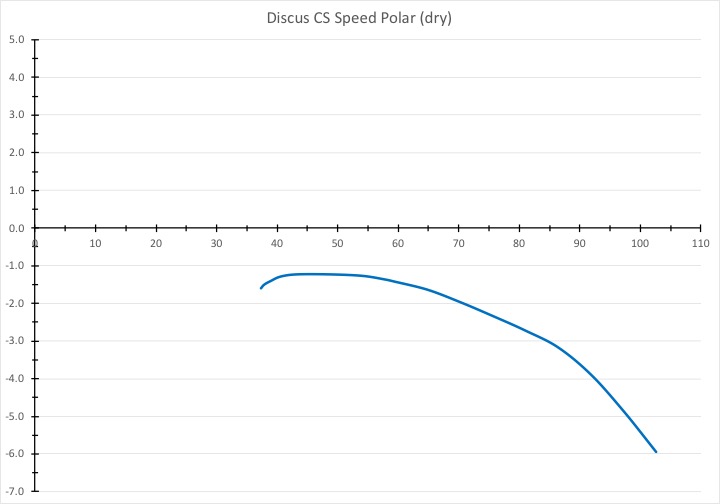
The next graph below shows that the best glide performance of the Discus CS is at about 55 kts. You can find this best glide speed by placing a tangent (the red line) against the speed polar starting at the chart’s origin (the point 0,0).
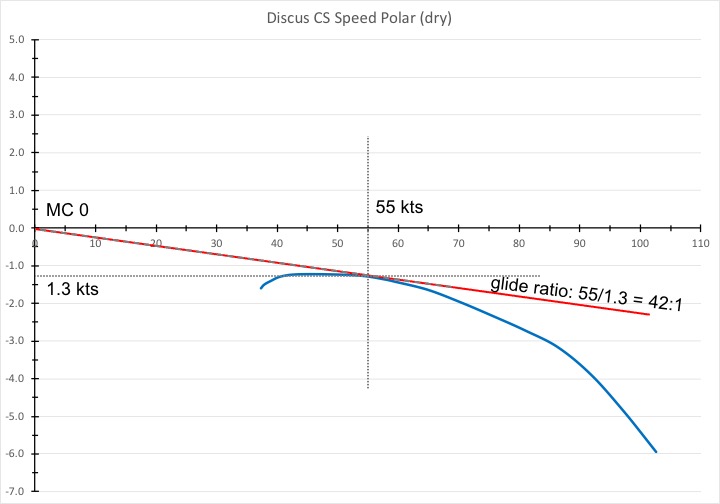
At 55 kts the Discus will sink at a rate of 1.3 kts. 55 divided by 1.3 equals 42. 55 kts is the best L/D speed for a Discus and its best glide ratio is 42:1.
The only time you would ever fly at the best glide speed is when you are desperate. Let’s say the lift has died for the day, the air is completely still, and you are just high enough to safely make it to an airport. That’s when you would fly at best L/D. This speed is also called MC 0 speed: the expected strength of the next lift is zero (because you know there is no more lift to be had) and all you are trying to do is to stretch your glide as far as possible.
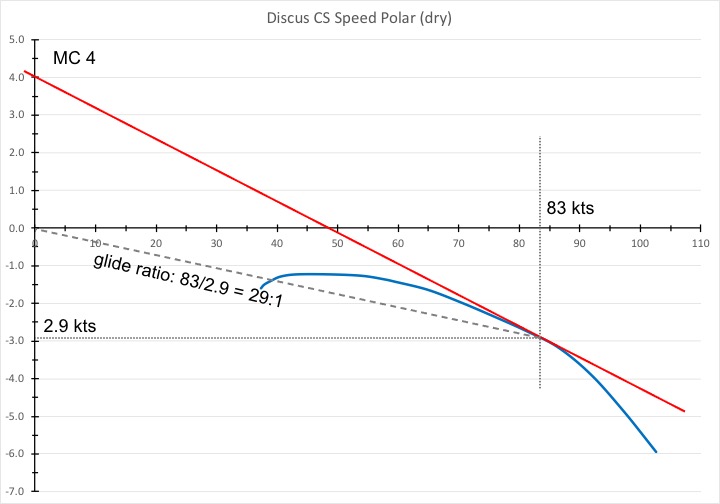
Let’s look at a more frequent example. It’s a pretty strong day. You are high and there are several good-looking cumulus clouds ahead. During the last few climbs you achieved 4-5 knots on average from the bottom to the top of each thermal (including any centering delays, re-centering efforts, etc) and you expect the next lift will be just as strong. In this case it makes sense to set your MC to 4. You expect the next lift to be just as strong and you are not willing to stop for anything less than that – at least for now. In this case you should fly at MC 4. (MC 3 or MC4 are perhaps the most common MC settings that pilots use for Speed-to-Fly calculations. Higher settings only make sense in exceptionally strong conditions. How often would you not take a climb that averages 4+ knots from bottom to top?)
You simply feed MC 4 into your vario and it will tell you to fly at MC 4 speed. The chart below shows you how your vario calculates this speed: it places a tangent (once again the red line) along the speed polar curve but this time it starts at a point 4 knots above the origin. The tangent touches the speed polar at 83 kts and you can see that at this speed the glider will sink 2.9 kts per hour. The glide ratio at this speed is 83/2.9 = 29. I.e. you will glide 29 ft forward for every 1 ft of altitude you lose. 29:1.
OK, so far, so good. You already knew this anyway. But what does this have to do with the headline? Where’s the peril? That’s what we’re getting to now.
The Other Use of the MacCready Value
The MC value that you enter is not only used by your vario to calculate your best Speed To Fly but it is also used by your flight computer to calculate whether you can safely reach a place to land.
I very much doubt that this was Paul MacCready’s idea. But that’s how your flight computer works. And if you don’t know it, it can be a big problem!
In the example we just discussed above it is hard to see. When you’re flying high and happy and are confident that the next thermal will deliver a 4 kt average climb you are probably not too concerned about reaching a safe place to land. And if you glance at your flight computer it will use your MC 4 setting to calculate which airports (or landout fields) are in safe glide at MC 4. I.e., it will do so based on a glide ratio of 29:1.
But let’s say the expected 4 kts of lift did not materialize. In fact, the clouds that looked so good before are now dissolving and you’re getting lower and lower. Far from being confident that the next lift will deliver 4 kts, you are gradually getting concerned. And, as you should, you dial back your MC settings. First to MC 3, then to MC 2, and, as you get lower and lower, you move it back to MC 1. Eventually you are getting desperate and dial it all the way back to MC 0.
This makes sense because you want your STF vario to tell you to fly more slowly so you better conserve altitude and have more options to find lift ahead, rather than driving hard down to the ground.
But what does your flight computer do with the same information? As you reduce your MC settings to 3, 2, 1 and then to 0, your glide computer thinks you can glide farther and farther. It basically removes your safety margin. Remember: at MC 0 your flight computer believes you are able to consistently fly at the very optimal glide speed – 55 kts in still air – and achieve a glide ratio of 42:1. Is this realistic? Probably not.
By reducing the MC value to 0 you just told the glide computer to lie to you. It is now showing airports (or fields) in glide range that really aren’t.
But things are probably even worse. Quite possibly much worse!
Unless the day has truly died and the air become completely still, chances are that the airmass you are flying through is actually going down. Why? Because as long as there are thermals and the air is going up somewhere, it must be going down elsewhere. Completely still air hardly ever exists and it most definitely does not exist on a day when we expect to find enough lift to fly cross-country.
So let’s say the air you’re flying through is actually going down by 1 kt. One knot is not much and definitely not unusual. What are the implications?
Well, first of all you should be flying a bit faster. When the air is sinking at 1 kt, your STF vario will tell you to speed up even if you leave your MC setting at 0. How does it do this? Easy: 1 kt sink will simply shift the glide polar down by 1 kt because you have to add the sink rate of the airmass to the sink rate of the glider. (The vario obviously knows you are in sink and it does this automatically. ) You can see the new polar on the chart below (in orange). You can also see where the tangent touches the new polar curve. This point is at 59 kts and your sink rate will now be 2.4 kts. (In still air it would be 1.4 kts but since you’re in 1 kt sink, so you’re actually coming down at 2.4 kts.)
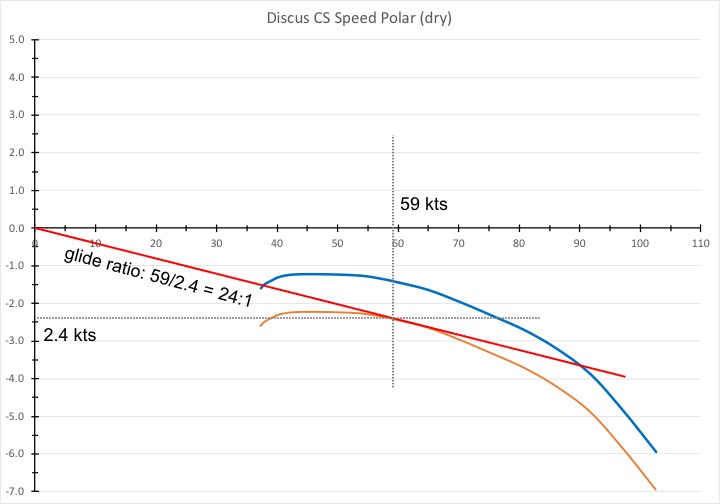
Now, look at what happened to the glide ratio! At 59 kts and 2.4 kts sink, your glide ratio is now 59/2.4 = 24:1. You’re still flying a high performance glider but just 1 kt of sink is enough to basically turn it into a Schweitzer 1-26!
What about the safety glide calculation? Your glide computer does not know how long the sink will last so it does not take it into account at all! (This makes sense because otherwise the safety glide calculation would jump around wildly each time you fly through a bit of lift or sink.) Remember this! The flight computer will account for wind (because wind doesn’t change from second to second) but it does not account for lift or sink when it calculates which airports (or fields) are in glide.
So what does it tell you? Since you turned down the MC value to 0, it will calculate your safety glide with a 42:1 glide ratio even though you are only achieving 24:1!
It is easy to see why this is at best misleading, and at worst a major safety hazard. A lot of beginning XC pilots tend to use what they think of as a “conservative”, i.e. low, MC setting. As long as this is only applied to Speed-to-Fly calculations it makes sense because it helps them stay high (while obviously slowing them down). But when applied to safety calculations a “low” MC setting is just the very opposite of conservative!
What Should You Do?
Now that you understand that your MC settings are used for two completely different purposes – calculating your speed to fly, and calculating your safety glides – what can you do about it?
The answer is simple: use two different MC settings, each appropriate for its purpose!
If your glider has an electronic Speed-to-Fly vario and you are also using a completely separate flight computer with a moving map, things are straightforward. For the vario use an MC setting that’s based on the minimum strength of the lift you are willing to accept. For the flight computer use an MC setting that’s appropriate for safety glide calculations.
This describes the setup that I was flying with last year. I had an STF vario in the panel and a stand-alone Oudie IGC flight computer with a moving map display. I entered my STF MC setting into the vario, and kept a different (usually higher) MC setting on the Oudie. This way the Oudie would only show me airports and fields that really were in safe glide range.
Things get problematic when your STF vario and your flight computer are connected with one another. Changes that you make to your MC settings on one device are probably automatically sent to the other device. The two devices are kept in synch. This seems like a great convenience but in reality it is anything but! In real life it is quite rare that you want to use the same MC value for your STF calculations and for your safety glide calculations. And whenever it is appropriate to use two different values than either of these two calculations will simply be wrong!
If you use a setup where your SFT vario and your flight computer are connected with one another (e.g. via cable or bluetooth), see if there is a setting that prevents the two devices from synchronizing MC values. You want each of these devices to correctly calculate the thing it is supposed to calculate!
If you only use only one single device for both STF and safety glide calculations (or if you cannot prevent your STF vario and your flight computer from synchronizing MC values) you must remember to edit your MC setting based on what you want to focus on. If you are relatively new to cross country soaring I suggest that you set the MC value appropriately for safety calculations and simply ignore your vario’s speed-to-fly suggestions. You’re probably not going to fly as fast anyway as the vario suggests you should.
And there’s one additional thing you should do: make sure that you complement a safe glide calculation by also setting a safe arrival altitude. After all, you don’t want to arrive at the airport (or field) at grass root level. You want to have enough time to do a proper landing check and fly a safe landing pattern. What’s a safe arrival altitude? That is a different question for another time. In Boulder, I always plan to arrive no lower than 1500 AGL because we have a very busy airport, and I may be in line behind other gliders or even a bunch of skydivers that are floating above the field just when I get there. Extreme weather can create problems, too. Here’s a scary experience from a few years ago.
What MC Value is Appropriate for Safety Glide Calculations?
We know from the MacCready theory how to set MC for Speed-to-Fly calculations: enter the expected lift of the next thermal. Better still (since you don’t really know how strong the lift ahead will be): enter the minimum strength of lift that you are willing to take right now.
But how to set MC for calculating safety glides? Well, as always, it depends. Since this calculation is about safety, and only about safety, the key question you should ask: given the looks of the conditions ahead, what is the “worst-case glide slope” with your glider in the direction you’re heading – at least until the next landable field or airport? Whatever your estimate is, you can then enter an MC value that corresponds to that glide slope.
OK, so how do you estimate your worst-case glide slope?
We have seen above that sink has a very negative impact on the attainable glide slope. Just 1 knot of sink will turn a 1:42 glider into a 1:24 glider. What about 2 knots of sink? Let’s take another look at the speed polar.
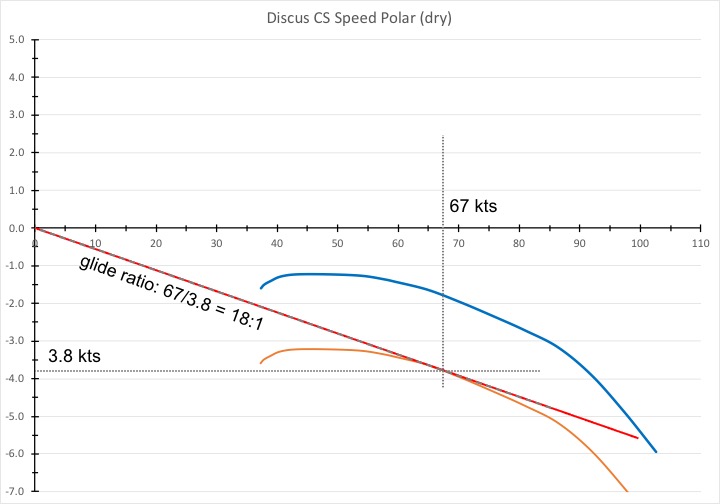
Two knots of sink will shift the speed polar down by – you guessed it – 2 knots. You’re in sink, so you must fly faster. How fast? Place a tangent from the origin against the new (orange) speed polar. 67 knots is the speed to fly and your rate of sink will be 3.8 kts. In the best case, this equates to a glide ratio of 18:1. (I say best case because it is pretty difficult to fly exactly at the right speed to fly and if you fly a little faster or slower, your glide ratio will actually be worse than 18:1.)
Depending on where you fly, two knots of sink still isn’t all that bad. Here in Colorado it is not uncommon to hit pockets of sink where the air goes down by 5 kts or even 10 kts. In wave conditions it could be as much as 20 kts! How would that affect your glide slope?
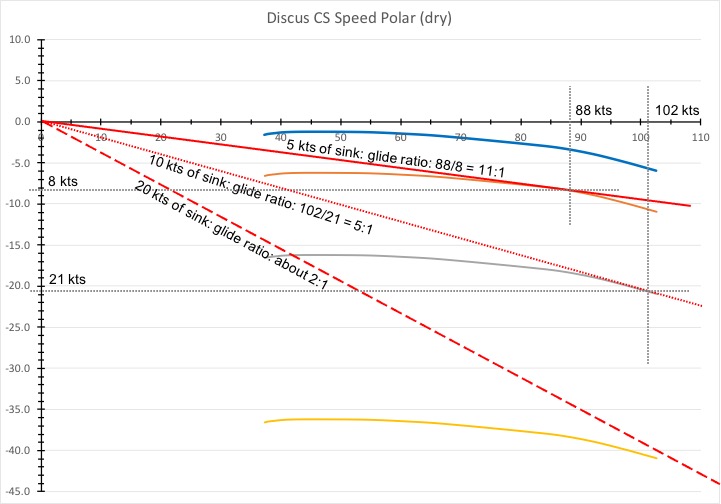
The chart above shows that the impact of strong sink is downright frightening. If you fly through 5 kts of sink your best glide ratio is 11:1 at a speed of 88 kts. If you cross 10 kts of sink, your best glide ratio becomes 5:1 at a speed of 102 kts. And at 20 kts of sink, the answer is literally off the chart. You’d fly somewhere between rough air speed and Vne and you’d be lucky to achieve much better than 2:1.
Scared? Well, you should be. Big sink is scary. If feels like you’re coming down like a brick. Because you are. Well, almost. Fortunately, strong sink tends to be short-lived. And since it’s true that what goes up must come down, it’s also true that what comes down must go up. Strong sink and strong lift tend to exist in close proximity to one another. Wave flying is an extreme example where 10-20 kt lift and 10-20 kt sink can be within 1 or 2 miles from one another. Try to get out of sink and back into lift as soon as possible! Hopefully you know what you’re doing! Or, perhaps even better: think twice before you decide to fly in such extreme conditions to begin with. The point is that such extreme scenarios are not really all that helpful when you decide how to program your flight computer.
In regular summer soaring conditions the more typical cases are that you’re getting low because the lift is weakening, that you fell out of the lift band, or that you crossed into a slowly descending airmass. In Boulder, Colorado, a classic example for the latter is that you fell out of the convergence, can’t get back, and are struggling to find good lift in the eastern airmass. A divergence zone running parallel to the convergence may put you in sink. In these cases you are unlikely to be confronted with sustained strong sink. But even in relatively benign conditions, it is still quite possible that you experience an average of 1 kt of sink on your final glide home.
Lets revisit the chart for 1 knot sink.
As we saw before, at 1 kt sink we should fly 59 kts and our glider will sink at a rate of 2.4 kts. Our glide ratio will be 24:1.
If this is the “worst-case glide-slope” that we are expecting, how can we instruct our flight computer to make the appropriate safety calculation? The answer is: we have to find the MC setting that corresponds to a 24:1 glide slope in the absence of lift or sink.
The following chart shows how we can do this easily.
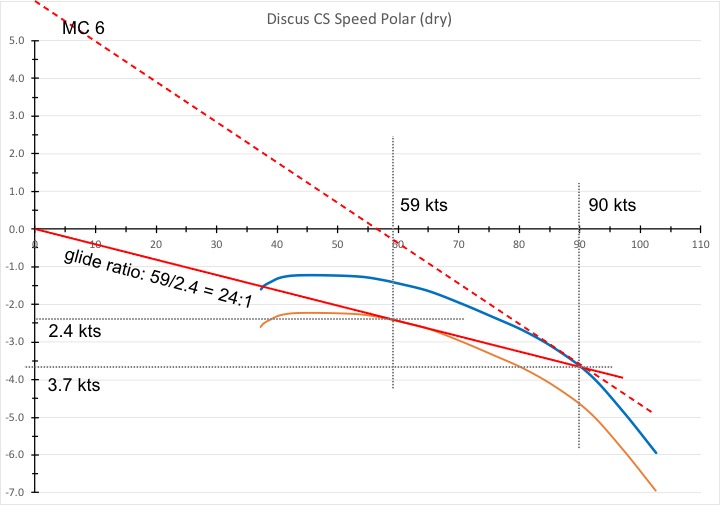
We simply look for the point where the 24:1 glide slope line (i.e. the red tangent to the orange speed polar) intersects the original (blue) still-air speed polar. We find that this point is at a speed of 90 kts and a sink rate of 3.7 kts. Now we draw a new tangent (the dotted red line) that touches the blue polar at exactly this spot. Then we check where this new tangent intersects the vertical axis. You can see that for the Discus this point is at 6 kts. In other words: if we expect a worst case glide slope of 24:1 all the way to the airport (i.e., conditions that reflect 1 kt of sink), we should set MC to 6.
You might be interested what MC setting I use. Once again, it depends! If there is a well-marked energy line ahead that I can follow, e.g. a cloud street or the typical Rocky Mountains convergence line, I am comfortable to base my safety glide ratio on an MC value as low as 3. If the sky is blue and I don’t really know what to expect I tend to use MC 4 or 5. And if the terrain is particularly hostile I bump it up to 6 or 7. Ultimately, it comes down to a judgement call. The more doubt I have about the conditions ahead and the greater the probability of sink, especially prolonged sink, the higher I set my MC value.
If you’re flying in particularly challenging terrain or if you’re not yet experienced in avoiding areas of persistent sink, you may want to follow the advice of the French mountain soaring team and use a “worst-case glide ratio” that is 1/2 of your gliders best glide performance. For the Discus CS this glide ratio is 21:1. The chart below shows that a Discus (without water ballast) will achieve 21:1 at a speed of 95 kts when the corresponding sink rate is 4.5 kts. And the corresponding MC value is about 10.
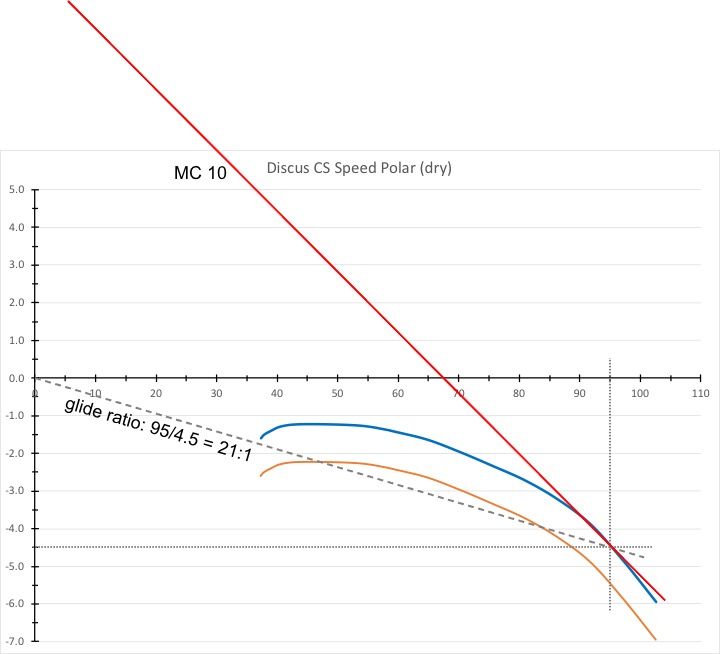
Remember that estimating a “worst-case glide ratio” is by no means a guarantee that reality may not be harsher yet. Perhaps even much harsher. I have shown above how bad a glide ratio gets if you hit 5, 10, or even 20 knots of sink!
Conclusion
The purpose of this article was to make clear that your glider avionics use MC for two completely different purposes and that applying inappropriate values can have dangerous unintended consequences.
Your STF vario uses MC to calculate the best speed-to-fly based on your assessment of the strength of lift ahead. If you’re conservative, you want this value to be lower, not higher. This will make you stay relatively high albeit at the expense of a somewhat lower cross-country speed. Irrespective of your level of experience, the most appropriate MC value is, “what is the weakest lift that I would be willing to accept right now.” MC 2, 3 or 4 are fairly typical. Only in exceptionally strong conditions will it be 5 or higher.
Your moving map flight computer uses MC to calculate which airports or fields are within safe gliding distance. If you’re conservative, you want this value to be higher, not lower. This will force you to stay high enough that you can safely reach your destination even if you should face less than favorable conditions ahead. Your skills, experience, the terrain, and the conditions of the day are all important factors to consider when you set this value. On benign summer days a value of MC 5 or 6 may be appropriate. If you’re inexperienced, flying over hostile terrain, or if you are unfamiliar with a particular soaring area, MC 10 will give you an extra safety margin. And always complement your glide slope calculation with a safe arrival altitude so you have the altitude you need for a safe landing pattern.
Importantly, set your MC values separately for your STF vario and your flight computer. Prevent these devices from synching their respective MC values if at all possible. Be very careful if you only use one device (or one synchronized input) for both calculations. The biggest trap exists when you dial back your MC setting for SFT purposes and your flight computer stretches your attainable glide unrealistically farther and farther.
Even the highest possible MC setting will not be appropriate to calculate safety glides when extreme sink, or strong sustained sink, is possible. When conditions are extreme, the best advice is to stay really high at all times. And if that’s not possible, or if you’re not sure you can deal with the conditions at the time, you can always decide to fly on a different day instead.
Have fun and fly safe!
Post Scriptum
There has been a lot of interest in this article. Within 48 hours of publication it has been read about 2,500 times and a lot of readers made excellent comments, either below or on social media.
First of all they confirm that the trap is real: entering a low MC value into your flight computer will result in wildly over-optimistic glide slope calculations and show fields or airports within glide range that really are not. However, there are multiple ways to avoid the trap and my suggestion in the article of using a different (and higher) MC value for safety glide slope calculations is only one of them.
Below I want to summarize a few comments that I found particularly helpful:
- If the terrain in your soaring area is generally landable there is not all that much to be concerned about. E.g., one pilot from the Netherlands commented that where he flies there are always several landable fields in glide even from as low as 1000 AGL. If that describes your soaring terrain then this topic doesn’t really apply to you. Your main challenge may be to resist the temptation to keep trying to find lift until you’re very close to the ground. Delaying the decision to land until it is too late for a safe landing is the #1 reason why glider pilots get killed. This is a different topic. You can read more about it here.
- As an alternative to using MC inputs for your final glide calculation you may be able to use “Required L/D”. E.g., I have my Oudie set up to display two Nav boxes at the top of the screen: “Required L/D” and “Current L/D”. As long as my “Current L/D” exceeds the “Required L/D” I am gaining relative to my required glide slope and my odds of making it to the target improve. Conversely, if the “Current L/D” drops below the “Required L/D” I am losing against my required glide slope and may be in trouble. This is a very useful method. If you use it, it is critical that you also complement it with a safe arrival altitude. In this video, I show an example of a final glide back to Nephi, Utah where I needed a glide ratio of 25:1 to get back to Nephi but then my “Current L/D” temporarily dropped to 18:1. (I was flying my 48:1 Ventus 2.)
- A lot of excellent pilots don’t use a “Speed-to-Fly” vario to tell them how fast to go. Instead they primarily rely on “block speeds.” E.g., if they are high and feel “confident” of finding good lift they will fly at a speed that roughly corresponds to their gliders STF at an MC setting of 4 in still air. If they are getting towards the bottom of the best lift band they become “conservative” and fly at a speed that corresponds to MC 2. And when they get “desperate” and are really looking for lift, they slow down to a speed corresponding to MC 1. And if they are “feeling lucky” high under a strong cloud street they fly extra fast. One of the commenters calls it “warp” speed. For a dry Discus CS these speeds might be: desperate: 60 kts; conservative: 65 kts; confident: 75kts; warp: ~85-90 kts. Add about 10 kts to each speed when flying with water ballast. If you like this method there is no need to mess with your MC value at all. Simply set an MC value on your flight computer that’s appropriate for your safety glides (combined with a safe arrival altitude) and leave it at that.
- Similarly, if you like your STF vario set to “netto” instead of “Speed-to-Fly” you also don’t need to bother meddling with MC values during the flight, and can just use an appropriate MC setting for safety glides on the flight computer.
- What MC value is appropriate for safety glides varies with the soaring terrain. My article was written from a mountain flying perspective. Where I fly in Colorado it is common that the next landable airport or field is 20, 30, 40, or even 50 miles away and soaring conditions tend to include strong lift as well as strong sink. Talk to experienced pilots in your area to understand what safety glide ratio (and hence what MC value) may be appropriate for where you fly.
Keep the comments and insights coming. Soaring is an unforgiving sport and our safety largely depends on our ability to learn from the mistakes others have made before us. (Or on sheer luck – but only for as long as it lasts.) By learning together we’ll become better and safer pilots.


Nice article. I use a LX8000 with an airport, waypoint and task page setup. This allows quick swopping between your task and possible two alternates during flight, on a single device. LX allows a navbox with the glide ratio to your target. I leave MC and arrival hight were it is and look at de required glide ratio to determine if an alternate is usable. With an 50:1 glider 20:1 works 99% of the time, 25:1 is a bit les confident and beyond 30:1 things “might” work, so have an alternate option more closely.
Like you said all depends on the conditions, at the end of the day with tailwind etc 35-40:1 could work just fine, just have a landable option in between. Also, my approach does not account for wind, so I have to choose an acceptable glide ratio accordingly.
Hi Halmar, thanks for your comments! I find that monitoring the actual glide slope is a good way to keep track of the conditions during the day and this may give me sense as to what glide ratio may be attainable. The main limitation is when I fly high and fast all day in the best lift band (for me often between 14,000 and 17,500 ft) and my final glide gets me through a very different airmass at much lower altitudes that I have not visited at all since the time of launch. In that case it is often a wild guess whether the final glide will be at 50:1, 30:1, 25:1, or even 100:1 – and yes, I have had even more than 100:1 🙂
Yes, here in the Netherlands the upper limit is FL055/FL065 depending on your exact location, and most days the weather is not good enough to reach even those levels. On the other hand there are virtually no places were there is not a landing option in reach from 1000ft. Completely different gliding. 🙂
I use 20:1 for the selection of the next out-landing site. Why 20:1, it is easy to calculate.
That works! 🙂
A nice article, exploring strategies that have been discussed and published for many decades. The early writings of Bruce Carmichael and Will Shumann come to mind, along with your more recent references.
Please note that Paul MacCready, as you stated, was a brilliant man. However, what you also stated- that he can get you in trouble- is not correct. He fully understood all of the subtleties you have explored in your article (and much, much more). If the way MC theory has been implemented in current technology does not fully reflect this, it is a shortcoming of application. Neither MacCready nor Nickel- who independently developed a similar theory in Europe- are getting anyone “in trouble”.
Regarding the recommendation to fly with two different MC settings and two different systems is one way to approach the issue you have discussed. A simpler method is to be familiar enough with your glider’s performance to know how much to slow down in steps as risk increases while holding the MC setting constant in a single flight computer. And how much to increase the speed in steps as things improve and as you get closer to final goal. The steps can correspond to single digit MC variances if that’s the easiest for you to work with. Adding more instruments, more technology, and more complication to the cockpit is not always the answer.
Hi Gary, many thanks for the thoughtful comments. I have nothing but respect for Paul MacCready and hopefully it is clear from the headline that I am not blaming him for the misapplication of his work. I tried to make this even more clear in the body of the text.
I have seen many pilots fly around with MC 0 or MC 1 believing that this keeps them safe without considering that it inadvertently results in wildly optimistic final glide calculations.
I agree with you that more technology is really not the right answer. However, the it’s a fact that the technology is already in most gliders and pilots use it whether they understand it or not. Especially for final glide calculations. And I believe it is vital that they understand how a low MC setting (which they believe makes them safer) is misleading when applied to final glide calculations, and that they take appropriate steps to avoid this trap. Thanks again!
Hey Clemens,
Great article! Completely agree with your general message.
With respect to specific safety values, I’d just like to note that the values (MC 5-6, MC 10) are probably overly conservative at many gliding sites. It’s easy to say that more conservative is better, but where I fly it would limit your options so much that you would hardly stay in glide of airports or perhaps better landing options. At flat, mostly landable East Coast sites, MC 3 is a reasonable bottom margin, 3.5 or 4 is reasonably appropriate as a conservative margin.
Completely agree though that if you are really banking on an option (heading away from the only landable airport toward a mountain!), that MC 6 or 7 is smarter for a safety glide!
Secondly, altitude arrival is another important safety factor (Eg: 1000ft). The reason is that when you are close, this is a stronger representation of margin than when you’re far away. 40 miles away, the angle difference between 1000 and 1500ft is almost nothing… MC represents most of your safety factor. But when you are 3 miles away, 500ft represents a very large difference in margin.
So the point is don’t forget to consider altitude of arrival as another dimension for safety factors.
All the best,
Daniel
Hi Daniel, very good points, as always!
Yes, the high values are intended to get to the nearest airport or the next landable field. This assumes that the terrain between the current position and the next airport or field is not landable.
As long as there are lots of fields to land within easy glide range and someone uses the computer just as a guide because they “would like to get home” then they can definitely back off and MC 3-4 will be just fine because 95% of the time it will be enough to make it.
In Colorado there very often aren’t any safe places to land and so these higher values really are necessary because of the other 5%. of cases when MC 3-4 does not cut it.
Thanks also for pointing out the safe arrival altitude. I edited the article earlier today to specifically include this. For all our club ships the policy is 1500 AGL minimum because we have a very busy airport and having to get in line for landing and/or waiting for a bunch of skydivers to float down under canopy is typical when you get back.
Best, Clemens
Hi Clemens,
I’m finally been getting into the details of my flight computer. Primarily I’ve been using XCSoar. Back when I was flying the club ships I had selected the polar appropriate to my glider in the flight computer and then calibrating my safety MacCready setting to give me 20:1 (I see Hans likes this value for its convenience too). This caused me to select a MacCready value of 5.8 or as high as 7.6 if I wanted additional margin! When I’d land away from the home field experienced folks would ask what safety MC I had selected that caused me not to attempt the jump back to the home field. I’d always get a quizzical look when answering 5.8 or above! Noob must be flying awfully conservative they must have been thinking.
When I started flying the HpH304CZ I calibrated the flight computer the same way. 30:1 = Safety MC of 5.8. Now after landing away from my home field and answering the same question with 5.8 more quizzical stares.
Of course this has everything to do with the level and shape of the default polars included with XCSoar. Are they correct? A quick comparison between published data, SeeYou, LXNAV, and XCSoar flight polars for my beloved 304 highlights they are somewhat different… especially the default XCSoar polar.
Asking which one is most accurate would stir up an endless discussion. What is more tangible is to realize that polars are modeled by 2nd order quadradic line fit. The MC setting that matches an L/D setting is very sensitive to the shape of the entire polar (of course).
By developing a customized polar (PRL file) I was able to much more accurately match the published non-ballasted data. The resulting glide ratios versus speed match what’s listed in the POH. Now when selecting a safety MC for 30:1, surprise, it’s more like MC=3.5… much more consistent with folks’ expectations.
Note also typically the profiles are quoted at 3 points to define the quadradic. For best results ensure all 3 points bound your normal operating flight speeds. Initially I’d selected the points to range between 40-65 kts for best accuracy at high L/Ds and included 5 points in the PRL file. This was a mistake since only the first 3 points are used by XCSoar’s internal curve fitting and the resulting error at speeds above 70 kts are strongly exaggerated by the curve fitting process. This again results in very high MC settings at ~30:1. I expect errors associated with poor selection of the 3 anchor points is not unique to XCSoar.
The consequence of flying with an inaccurate polar shape but appropriately calibrated safety MC is inaccurate STF values. Not really a safety concern, but also not inspiring confidence in your flight computer. This would be noticeable in still air by consistent and strong speed oscillations necessary to hold the STF on target. Since you’ve done a fine job of summarizing all this I figured I share here for the benefit of others.
Cheers,
Taylor
Hi Clemens,
Thanks for this great explanation.
Just wanted to add, both LX flightcomputers (LX80XX en LX 90X0) and XCSoar have Safety MC features that help with uncoupling the STF-MC from the glide calculations.
Don’t think Oudie/SeeYou Mobile has a similar function though, and personally think the way LX implemented it isn’t great either.
This video explains the way LX implemented it:
https://www.youtube.com/watch?v=hPDj59BgIk0
Best,
Dinant
Hi Clemens, and thanks for your reflexion,
I would not go up to say that dear Mr. MacCready can get me in trouble, because we always keep in mind that a good safety arrival altitude margin and monitoring that required L/d to goal is never higher than say 20:1 could give the same effect.
But definitively, your article is great to understand why the notion of « Safety Mc » is born and incorporated by Lx instruments or apps like XcSoar. This is the right way to have a Mc setting for STF and an other one to calculate a safer final glide to field.
Like Clemens mention, the Dave Springford (FoxOne corp) video
https://www.youtube.com/watch?v=hPDj59BgIk0
Is really a must, to a good understanding of how to set Safety Mc or Safety Mc Offset. You will find that if Safety Mc is set to a lower value than your current Mc, then, you will really be in trouble.
Denis
mu7g9z
Does anyone else calculate their glide ratio into more usable units? 42:1 is cumbersome when the units for altitude and distance aren’t the same, so one of the first things I do in a new glider is convert the glide ratio into nautical miles (the units I’m accustomed to and what the airspeed indicator uses) per thousand feet
hello!,I relly like your writing very a lot! proortion we keeep up a correspondence extra about your post on AOL?
I reequire a specialikst in this splace to solve my problem.
Maybe that’s you! Looking ahead too seee you.
Wonderfully written. Thank you. May I suggest two minor corrections?
The first is just a typo: there should be no “t” in “Schweizer” when you say “just 1 kt of sink is enough to basically turn it into a Schweitzer 1-26!”
The second suggestion is to remove “per hour” where you say “the glider will sink 2.9 kts per hour. ” As you pointed out earlier, a knot is a nautical mile per hour. Here, the correct units for the sink rate is “knots”, not “knots per hour”.
vt86dk