What is Wave Lift?
Every soaring textbook explains that under certain conditions wave lift forms on the lee side of a mountain range when the wind blows right across it. Usually this is illustrated with a graphic like this:
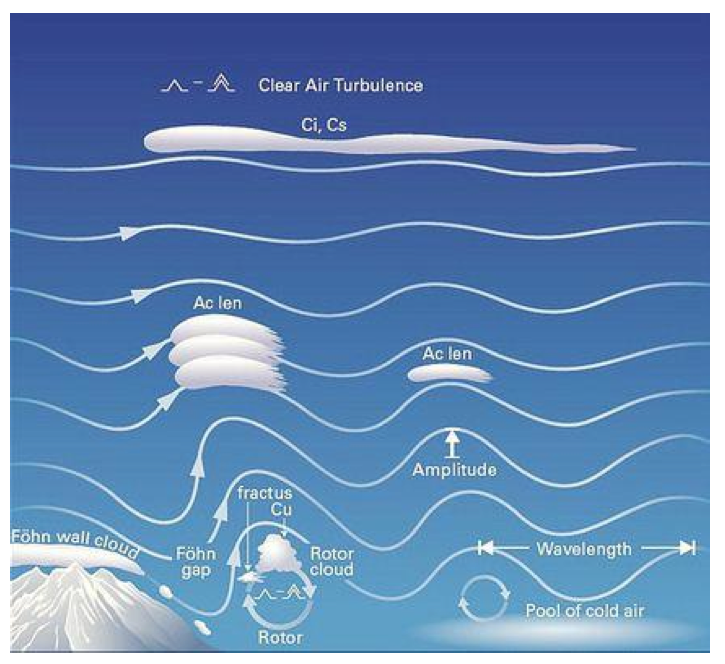
The picture shows the air oscillating (i.e., repeatedly moving up and down) right behind the mountain range until the air flow returns to equilibrium.
It is fairly intuitive to understand that air blowing down a steep mountainside eventually has to rise again. However, it is less intuitive, why the upwards movement is so pronounced (after all, air moving up behind a mountain range can reach altitudes that are several times higher that the mountain range itself). And it is also not intuitive, why the airflow continues to oscillate such that there is a secondary wave, a tertiary wave, and so forth. Many articles on the subject don’t really explain why the air continues to move up and down, i.e., how these oscillations come about. In addition, I remember asking myself a lot of other questions pertaining to wave lift. So I decided to sift through various text books and try to answer each of the following questions here for myself.
So why does the air move up and down?
Imagine a day hiking in the mountains. Assume that the day’s conditions are such that the ambient air temperature cools at a rate of 0.6 degrees Celsius per 100m (that’s the equivalent of 1.8 degrees Celsius per 1,000 feet).
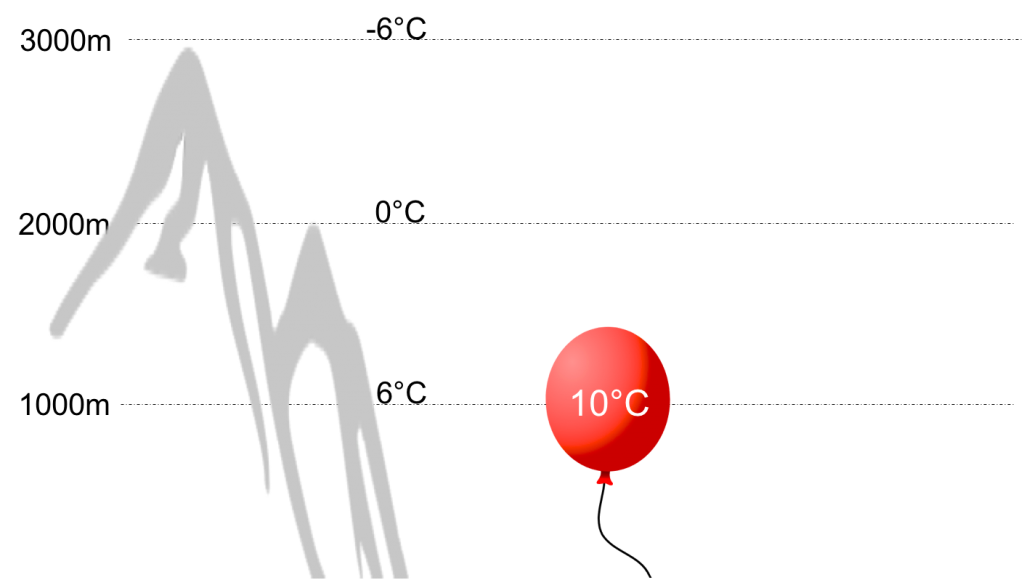
You have climbed to an altitude of 2000m. Let’s say the ambient air temperature is just around freezing (i.e. 0 degrees Celsius). The temperature at 1000m (where you may have started your hike) was six degrees warmer (i.e. +6 degrees C) and the temperature at 3000m (where you might be headed next) is another six degrees colder (i.e. -6 degrees C).
So now imagine you stop at 2000m to fill up a big balloon with the ambient air such that the temperature in the balloon will be the same temperature as the one surrounding you. Then you seal the balloon so that the air inside won’t mix with the air outside. (Also assume that the balloon skin is infinitely elastic, i.e. that it expands and contracts without creating additional pressure on the air inside; I know this is not realistic but go with it! The point is just to ensure that the air inside the ballon and the air outside don’t mix.)

Next you carry the filled and sealed ballon down to an altitude of 1000m. Here comes the key question: what temperature has the air inside the balloon that you have just brought down to 1000m?
If you have guessed that it stayed at 0 degrees C you would be just as wrong as if you had guessed that it warmed to 6 degrees C. And it didn’t warm to anything in-between either.
The temperature inside your infinitely elastic balloon will have risen at the Dry Adiabatic Lapse Rate (DALR) to almost 10 degrees Celsius! The DALR is a constant and is always 9.8 degrees Celsius per 1000m (which is the same as 3 degrees Celsius per 1000 ft). (The DALR depends only on the specific heat capacity of air at constant pressure and the acceleration due to gravity.)
So there we have it: we are now at 1000m and the air in our balloon has 10 degrees C while the surrounding air temperature is still 6 degrees C.
Imagine we now let go of our balloon (assume that the skin is not only infinitely expandable but also weightless). What will the balloon do? Well, now things are becoming more intuitive. The air inside the balloon is much warmer (and lighter) than the ambient air at 1000m. Hence, the balloon will immediately start to rise.
As it rises the air inside it will cool again at the same dry adiabatic lapse rate. I.e., when the balloon is back at 2000m the air inside will once again be zero degrees Celsius, the same temperature as the air surrounding it. However, our balloon won’t suddenly stop rising. It has gained a lot of momentum on its way up from 1000m and its inertia will force it to overshoot and continue to climb.
As it does so, the air inside will continue to cool at the DALR. Assume for a moment that it overshoots all the way to 3000m. (We’ll get to how far it may overshoot and why.) When it reaches 3000m and finally stops ascending, the air inside will have cooled down to -10 degrees Celsius. Since the surrounding air at that altitude is much warmer (-6 degrees Celsius), the balloon will begin to descend again. When it reaches 2000m, the air on the inside will once again have warmed to 0 degrees but the balloon’s inertia will force it to descend further and the air inside will continue to warm at a faster rate than the surrounding airmass. Eventually the downward movement will stop. But at that point the air inside will once again be warmer than the surrounding air and it will start to rise again. Just like a pendulum (that is not supported by a weight or spring), it will tend to overshoot less and less with each up or down movement and eventually the oscillations will come to an end.
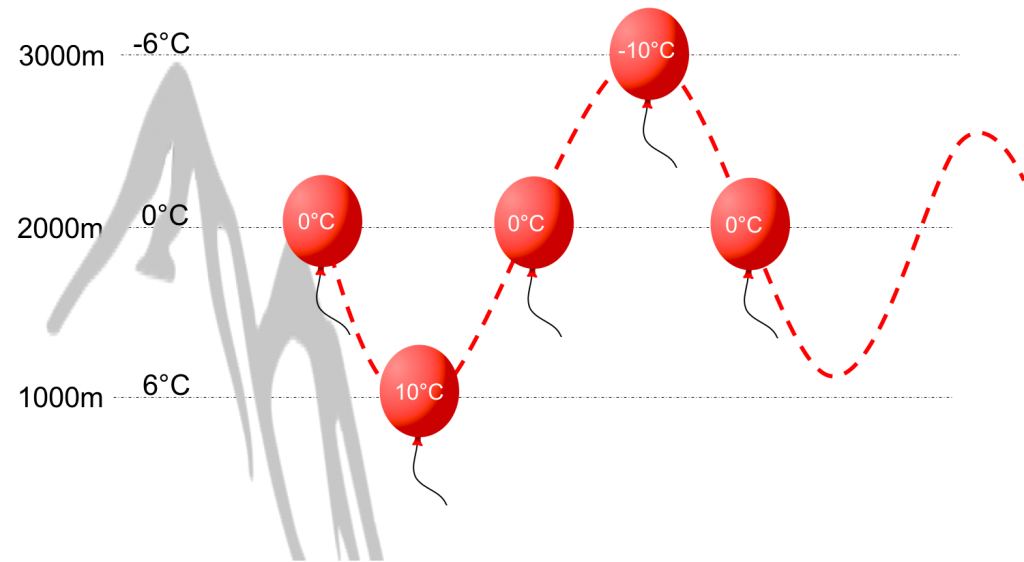
Our example with the balloon has made it clear that temperature differences between a displaced airmass (inside the balloon) and the surrounding air are causing these oscillations. Thereby it also illustrated one very important conditions for wave to occur: the ambient air must be “stable” for those oscillations to be possible. In other words: the Environmental Lapse Rate (ELR) must be smaller than the DALR.
If the ELR were identical to the DALR, moving the balloon up and down would not cause a temperature difference between the air inside it and the surrounding airmass. In our example, moving the balloon from 2000m to 1000m would obviously still increase the temperature inside the balloon from 0 degrees C to 10 degrees C (remember the DALR is a constant). But if the surrounding air at 1000 m was also 10 degrees C, the balloon would just stay were it was if the surrounding air had also warmed to 10 degrees C. And if we moved the balloon further up, it’s inside temperature would also always be the same as the surrounding air temperature, so there would never be an impetus for the balloon to move up or down on its own.
If the ELR were bigger than the DALR, i.e. the surrounding air was unstable, than the balloon’s vertical momentum would accelerate in whatever direction it was initially displaced.
So we remember that one critical precondition for wave oscillations is a stable surrounding air mass characterized by an the environmental lapse rate that is smaller than the dry adiabatic lapse rate: i.e.: ELR < DALR.
What triggers mountain wave?
In our balloon example, the wave oscillations were triggered when our hiker took the balloon filled with 0 degree air at 2000m and displaced it by carrying it down to 1000m.
So, in order to trigger wave, we need a force that causes stable air (i.e., air that naturally resists moving up or down because its ELR is less than the DALR) to be displaced from its original altitude.
In the case of mountain lee wave it is the wind and the mountain that do the displacing. Wind blowing against a mountain range lifts the air on the windward side and brings it down on the leeward side. It is this rapid downward movement of the air on the lee side that causes the displacement (and quick warming of the air on its way down).
Obviously the air is not enclosed by a balloon but in sufficiently strong winds the rapid downward movement along a mountain slope does not allow for a mixing of the displaced air with the surrounding air mass.
Because we are dealing with a stable air mass, the displaced air flowing down the mountain will be much warmer that the surrounding air once it reaches the valley at the foot of the mountain. It will then begin to rise because it is much lighter than the surrounding air.
So we remember that for mountain wave conditions to arise, strong winds have to blow across a mountain range and displace a stable air mass along the downward slope in the lee of the mountain.
The displaced air will then begin to rise rapidly. As long as it is warmer than the surrounding air, it will gain momentum. As it rises, it will cool at the DALR, and, because of inertia, it will overshoot the point where it reaches the same temperature as the ambient air. Eventually its ascent will come to a halt. But at that point the ambient air will be warmer than the parcel that just moved up and hence it will begin to move down again. The parcel will continue to move up and down, each time overshooting the equilibrium point due to its upward or downward momentum. Further downstream of the mountain the oscillations will continue to dampen until the temperature equilibrium with the surrounding air is reached and the oscillation stops.
What is a Wave’s Amplitude and What is its Wavelength?
Waves can be characterized by their amplitude and wavelength. Both characteristics are important for soaring.
The amplitude is the height of the wave measured from its midpoint (where the upward moving air has the same temperature as the surrounding air mass) to the top of the wave (where the upward moving air tops out and begins to move down because it is now colder – and therefore heavier – than the surrounding air). The amplitude of a particular wave depends on the topography (the height and shape of the downward mountain slope), and also on the strength of the wind (the stronger the wind the greater the amplitude) and the stability profile of the air (the more stable the air, the greater the amplitude).
The wavelength is the (horizontal) distance between the top of the wave crest and the top of the adjacent wave crest. The wavelength mainly depends on the stability profile of the air and the strength of the wind: the stronger the wind, the longer the wave length (the air travels farther from crest to crest if the wind is strong). Likewise, the weaker the stability profile (at a given wind speed), the longer the wave length will be (because in less stable air the temperature gap between the displaced air and the surrounding air will be less, therefore the impetus of the displaced air to quickly return to the equilibrium will be less). Mountain waves tend to have a wavelength anywhere between 3 and 30 kilometers.
The strongest lift for soaring will occur when the wave length is short and the amplitude is very high. Relatively strong winds moving a very stable air mass directly across a high mountain range along a steep downward slope will generate such strong conditions.
Read Next: How is mountain wave triggered?

