Since ridge lift requires two key ingredients – a slope and the wind – the key variables that determine the nature and strength of ridge lift are the shape and incline of the slope, the strength of the wind, and the angle at which the wind blows at the slope. In addition, it’s also useful to consider the stability profile of the airmass.
- What’s a good slope for ridge lift?
To produce optimal lift, the slope has to be shaped in a way that the wind will blow up along the slope and not around it. Consider the following slopes:
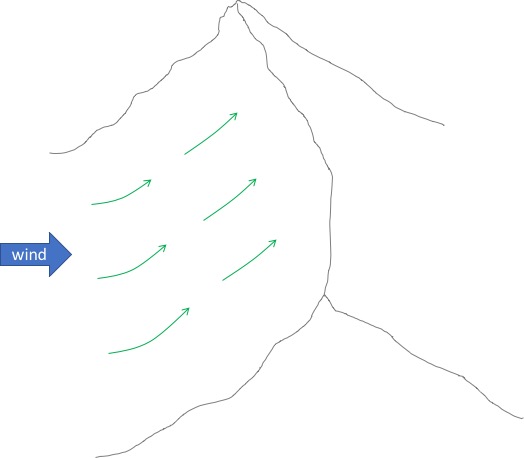
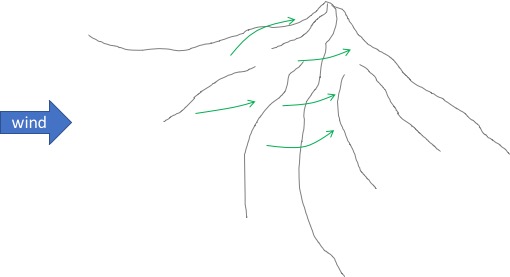
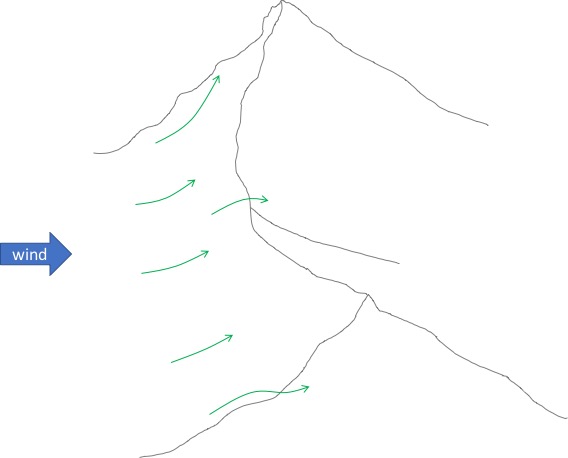
If you look at these slopes it should be quite intuitive that Slope A will produce the best ridge lift: the wind is trapped in a bowl and can’t go anywhere but up. Slope C has some similarities with slope A but the bowl is on the backside of the ridge. On the windward side it is shaped towards the wind, so the wind will have a tendency to move around it. Slope C might still produce usable lift but nowhere near as strong as Slope A. Slope B is the worst of the three. The wind always has a tendency to take the path of least resistance so it will mostly flow around the peak. However, if the isolated peak is a big mountain, then its windward facing slope may be large enough to prevent the wind from going around it and still produce decent usable lift.
- What role does the incline of the slope play in creating ridge lift?
Steep slopes deflect the wind in a more vertical direction, hence they will produce better lift than shallow slopes. You can easily picture this if you think of the wind blowing along the slope as a vector and deconstruct it into its vertical and horizontal components.
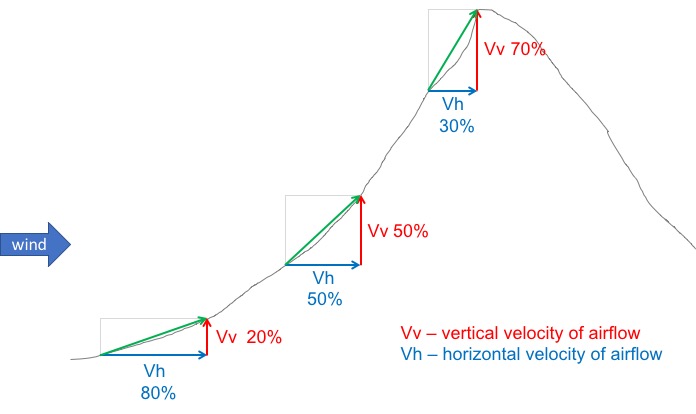
Along the shallower parts of the slope, the vertical component of the airflow might be 20% of the total, whereas at the steepest section it may be as much as 70% (see graph above).
Let’s say the wind blows with a constant speed of 10 kts against the slope. In this case we might expect the strength of the ridge lift to be 2 kts (20% of 10 kts) at the shallower section of the slope (usually at the bottom), and as much as 7 kts (70% of 10 kts) at the steepest section of the slope (usually towards the top).
Note that the horizontal component of the wind is the speed at which the glider flying parallel to the ridge will drift towards the mountain. It determines the crab angle that is necessary to maintain a safe distance from the ridge (more on this later).
Note that the wind speed is hardly ever constant and varies along the slope – based on the overall wind conditions as well as local factors such as the valley breeze and thermodynamic heating of the ridge in the sun (anabatic flow).
It is also useful to consider the airflow further away from the slope. This will help us estimate how high the lift might reach above the ridge. To do that we have to imagine streamlines of air across the mountain.
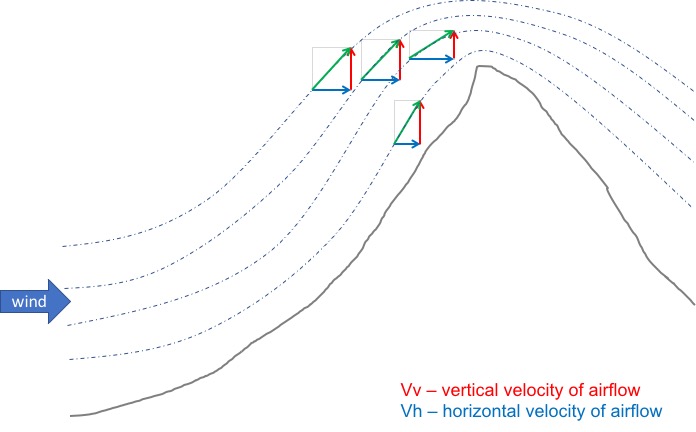
Note how the streamlines get compressed near the top: the wind seeks the path of least resistance and will not rise higher than necessary. (Hikers know from experience that the top of the ridges are usually the windiest spots and this is the reason why.) The best climb rates are usually just below the top of the ridge on the windward side – where the wind is still forced upwards.
- How strong should the wind be?
The illustrations above clearly demonstrate that – at least in theory – the stronger the wind the stronger the lift. However, ridge soaring can get extremely rough and quite dangerous if the wind is howling over the ridges.
The sweet spot for ridge soaring tends to be when the surface wind speed is around 15-20 kts. 10 kts is often sufficient – especially in suitable and steep terrain (see above). Conditions tend to get very rough at wind speeds of 25-30 kts or above. The reason is that the amount of turbulence increases with the square of the wind speed. So if you double the speed of the wind from 20 kts to 40 kts, the turbulence will be four times stronger.
- What’s the best wind direction?
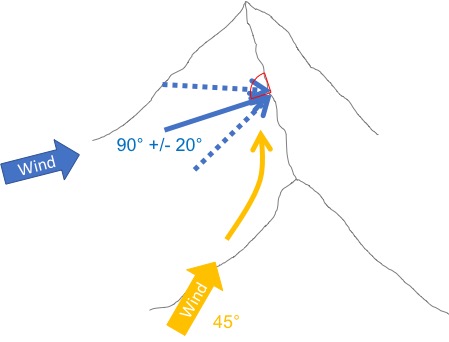
As one would expect, the best ridge lift can be expected when the wind blows directly against the ridge, i.e. if the angle between the wind direction and the ridge is 90 degrees. Deviations from perpendicular by plus/minus 20 degrees on either side will generally work well also. However, when the angle becomes more acute the ridge may no longer produce usable lift. The obvious reason is that the perpendicular component of the wind is reduced the more acute the angle becomes. E.g., a 45 degree wind will reduce the component that is perpendicular to the ridge by about 30%. In other words, with wind blowing at a 45 degree angle against the ridge, the wind speed needs to be at least 30% higher to generate the same amount of lift. Another factor is even more important: as mentioned before, the wind will seek the path of least resistance. In this case this means that the more acute the angle of the wind to the ridge, the more likely it is that the ridge will simply deflect the wind along the ridge such that it now flows parallel to the ridge and not over it.
In real life it is rare to find ridges that are completely straight. In most cases ridge lines are complex and dotted with bowls and spurs.
In ridge soaring it is important to always know the direction of the wind and to carefully observe the terrain to visualize where the wind will be forced upwards (and – conversely – where one is likely to find strong turbulence and sink).
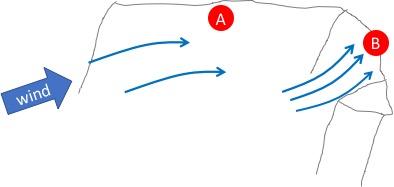
In the sketch above, the wind strikes ridge A at an acute angle and is deflected along the ridge until a spur protruding to the front from part B of the ridge blocks its path and it is funneled upwards along part B of the ridge.
- How is the stability profile of the air relevant for ridge soaring?
Ridge soaring is more predictable if the air mass is stable. In stable air, the wind and the shape of the terrain are the only two factors to consider. This can be difficult enough, especially in complex terrain. If the air mass is unstable, ridge lift will often be disrupted by (usually invisible) thermals breaking off from the ground. This can add to the overall climb rate, especially along slopes that are directly exposed to the sun, but it can also cause sudden and unexpected turbulence and sink between thermals in areas where we would expect air moving up along a slope. The more unstable the air mass, the wider the safety margin needs to be when flying along a ridge.
To understand the root cause of these implications we must remember the difference between stable and unstable air masses.
Air is stable if a parcel of air that is moving up (e.g. because it is forced up along a slope by the wind) cools faster (and therefore becomes colder) than the surrounding air as it ascends. Remember that the parcel moving up along the slope will always cool at the Dry Adiabatic Lapse Rate (assuming that there are no clouds along the slope). The DALR is a constant and always 9.8 degrees C per 1,000 meter (this is the same as 3 degrees C per 1,000 feet). Whether the air mass is stable or not therefore depends on whether the temperature of the air mass itself, i.e. the actual Environmental Lapse Rate (ELR) decreases slower or faster than the DALR.
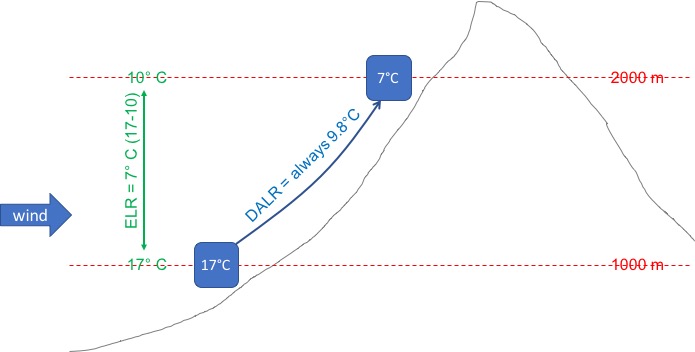
In the example above the parcel of air that is being forced up the mountain by the wind cools from 17 degrees C to 7 degrees C. It always cools at the DALR (if there are no clouds) and the DALR is always and everywhere 9.8 degrees C per 1,000 meter. The surrounding air at an altitude of 2,000 meter is 10 degrees C, i.e. 3 degrees warmer because the ELR on this particular day and at this particular altitude is 7 degrees C per 1,000 meter. So: because the ELR on this particular day and at this particular altitude is less than the DALR, the air mass is stable.
Conversely, we would be dealing with an unstable air mass if the parcel of air moving up along the slope were to remain warmer than the surrounding air mass: it would continue to rise until it would get to a stable layer where its ascent would then be gradually stopped (it may overshoot due to inertia).
Stable air will only ascend if it is forced to do so by the wind and the terrain. If you know the direction of the wind relative to the terrain in front of you, it is therefore fairly predictable. However, there’s also a downside to this: stable air will descend rapidly behind the crest of the ridge (because it is cooler and therefore heavier than the surrounding air). Under such conditions we can expect very strong sink and heavy turbulence on the leeward side of the ridge.
If the air is stable, the wind is strong, and the terrain is suitable on the lee side of the ridge, these are the perfect conditions for mountain lee waves to develop.

